Next: 20.5 Komplexe Kurven-Integrale Up: 20 Mehrfach Integrale Previous: 20.3 Integrationsmethoden
20.4.1 Satz von Frobenius
für totale Differential-Gleichungen.
Es sei
![]()
![]() für irgendein
für irgendein
![]() .
Dann existiert lokal eine differenzierbare
Lösung
.
Dann existiert lokal eine differenzierbare
Lösung
![]() der totalen Differentialgleichung
der totalen Differentialgleichung
Bemerkung.
Für
![]() sei
sei
![]() , dann ist
die totale Differentialgleichung
, dann ist
die totale Differentialgleichung
![]() gleichbedeutend
mit
folgendem
System partieller Differentialgleichungen
gleichbedeutend
mit
folgendem
System partieller Differentialgleichungen
Beweis.
![]() Für
Für
![]() sei
sei
![]() eine lokale
Lösung obiger Differentialgleichung mit Anfangsbedingung
eine lokale
Lösung obiger Differentialgleichung mit Anfangsbedingung
![]() .
Dann ist
.
Dann ist
![]() stetig und
nach der Kettenregel ist
stetig und
nach der Kettenregel ist
![]()
![]() mit
mit
![]() Es sei
Es sei
![]() fix.
Wir führen die totale Differentialgleichung
auf eine gewöhnliche zurück.
fix.
Wir führen die totale Differentialgleichung
auf eine gewöhnliche zurück.
Es sei
![]() fix.
Wir nehmen vorerst an, daß eine lokale Lösung
fix.
Wir nehmen vorerst an, daß eine lokale Lösung
![]() der totalen Differentialgleichung mit Anfangswert
der totalen Differentialgleichung mit Anfangswert
![]() existiert und setzen
existiert und setzen
![]() .
Dann gilt
.
Dann gilt
Wir betrachten nun den Spezialfall, wo
![]() nur vom ersten Faktor abhängt:
nur vom ersten Faktor abhängt:
20.4.2 Folgerung.
Stammfunktion im Mehrdimensionalen.
Es sei also
![]()
![]() . Dann ist
. Dann ist
![]() es existiert lokal ein
es existiert lokal ein
![]() mit
mit
![]() und
und
![]() , d.h.
, d.h.
![]() ; also ist
; also ist
![]() lokal eine
Stammfunktion von
lokal eine
Stammfunktion von
![]() .
.
20.4.3 Definition. 1-Form.
Eine 1-Form ist eine Abbildung
![]() . Sie heißt
exakt, falls
es eine Stammfunktion auf ganz
. Sie heißt
exakt, falls
es eine Stammfunktion auf ganz
![]() , d.h. eine
differenzierbare Abbildung
, d.h. eine
differenzierbare Abbildung
![]() gibt, mit
gibt, mit
![]() .
.
Wenn
![]() differenzierbar ist, dann schreibt man auch
differenzierbar ist, dann schreibt man auch
![]() für die exakte 1-Form die durch die Ableitung
für die exakte 1-Form die durch die Ableitung
![]() gegeben ist.
Für
gegeben ist.
Für
![]() und die lineare Koordinatenprojektion
und die lineare Koordinatenprojektion
![]() erhält man insbesonders die exakte 1-Form
erhält man insbesonders die exakte 1-Form
![]() die an jeder Stelle durch
die an jeder Stelle durch
![]() gegeben ist.
gegeben ist.
Eine allgemeine 1-Form
![]() kann für
kann für
![]() nun wie folgt geschrieben
werden:
nun wie folgt geschrieben
werden:
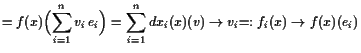 |
||
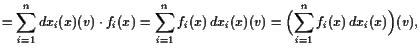 |
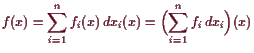
Ist
![]() , dann ist
, dann ist
![]() , also
gerade die
, also
gerade die
![]() -te partielle Ableitung von
-te partielle Ableitung von
![]() und
und
20.4.4 Theorem. Exakte
1-Formen.
Es sei die 1-Form
![]() exakt und
exakt und
![]() . Dann ist
. Dann ist
Eine Menge
Beweis.
![]() Der Satz von Frobenius liefert uns nur eine lokale Stammfunktion.
Der Grund dafür war, daß im Beweis
Der Satz von Frobenius liefert uns nur eine lokale Stammfunktion.
Der Grund dafür war, daß im Beweis
![]() eine lokale Lösung
einer gewöhnlichen Differentialgleichung war.
Da im vorliegenden Fall
eine lokale Lösung
einer gewöhnlichen Differentialgleichung war.
Da im vorliegenden Fall
![]() aber nicht vom Faktor
aber nicht vom Faktor
![]() abhängt, ist die
entsprechende Differentialgleichung:
abhängt, ist die
entsprechende Differentialgleichung:
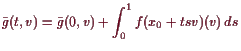 für
für 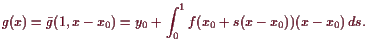
Wenn
![]() exakt ist, dann können wir die Stammfunktion
exakt ist, dann können wir die Stammfunktion
![]() von
von
![]() auch direkt
one den Satz von Frobenius wie folgt bestimmen:
auch direkt
one den Satz von Frobenius wie folgt bestimmen:
20.4.5 Proposition.
Stammfunktion via Kurvenintegral.
Es sei
![]()
![]() .
Dann ist
.
Dann ist
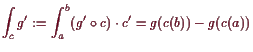 für alle
für alle
Beweis. Nach Kettenregel und Hauptsatz gilt:
![\bgroup\color{demo}$\displaystyle \int_a^b (g'\o c)(t)\cdot c'(t) dt =
\int_a^b (g\o c)' = g(c(b)) - g(c(a)){\rm\quad[]}
$\egroup](img3504.gif)
Dies führt dazu auch für allgemeine 1-Formen
![]() das Integral längs Kurven
das Integral längs Kurven
![]() wie folgt zu definieren:
wie folgt zu definieren:
20.4.6 Definition. Kurvenintegral.
Es sei
![]()
![]() und
und
![]() eine stetige 1-Form.
Dann ist das Kurvenintegral
eine stetige 1-Form.
Dann ist das Kurvenintegral
![]() wie folgt definiert:
wie folgt definiert:
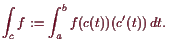
20.4.7 Proposition.
Reparametrisierungsinvarianz des Kurvenintegrals.
Das Kurvenintegral ist Reparametrisierungs-invariant.
Es sei
![]()
![]() und
und
![]()
![]() mit
mit
![]() und
und
![]() , und
, und
![]() eine stetige 1-Form.
Dann ist
eine stetige 1-Form.
Dann ist
Beweis.
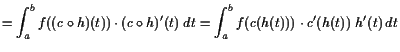 |
||
![$\displaystyle = \int_{h(a)}^{h(b)} f(c(s))\cdot c'(s)\; ds{\rm\quad[]}$](img3516.gif) |
20.4.8 Theorem. Exaktheit via
Wegunabhängigkeit.
Es sei
![]() eine stetige 1-Form auf einer
zusammenhängenden offenen Menge.
Dann ist
eine stetige 1-Form auf einer
zusammenhängenden offenen Menge.
Dann ist
![]() genau dann exakt, wenn
ihr Kurvenintegral wegunabhängig ist, d.h. nur von den Endpunkten der Kurve
und nicht ihres Aussehens dazwischen abhängt.
Als Stammfunktion können wir
genau dann exakt, wenn
ihr Kurvenintegral wegunabhängig ist, d.h. nur von den Endpunkten der Kurve
und nicht ihres Aussehens dazwischen abhängt.
Als Stammfunktion können wir
![]() definieren, wobei
definieren, wobei
![]() eine
eine
![]() -Kurve von
-Kurve von
![]() nach
nach
![]() ist.
Weiters ist die Stammfunktion bis auf eine additive Konstante eindeutig.
ist.
Weiters ist die Stammfunktion bis auf eine additive Konstante eindeutig.
Definition.
Eine offene Menge
![]() heißt zusammenhängend
heißt zusammenhängend
![]() zu je zwei Punkten
zu je zwei Punkten
![]() existiert ein Polygonzug, welcher
die beiden Punkte verbindet.
Wenn
existiert ein Polygonzug, welcher
die beiden Punkte verbindet.
Wenn
![]() Kurven sind, die an den Endpunkten
übereinstimmen (d.h.
Kurven sind, die an den Endpunkten
übereinstimmen (d.h.
![]() ),
so definieren wir die Kurve
),
so definieren wir die Kurve
![]() durch
durch
![]() . Ein Polygonzug ist also
. Ein Polygonzug ist also
![]() ,
wobei die
,
wobei die
![]() die affinen Verbindungsstücke der Ecken sind.
die affinen Verbindungsstücke der Ecken sind.
Die Segmente
![]() des
Polygonzugs können durch
des
Polygonzugs können durch
![]()
![]() -parametrisiert
werden. Die Ableitungen an der Ecken stimmen aber nicht überein, also liefert
-parametrisiert
werden. Die Ableitungen an der Ecken stimmen aber nicht überein, also liefert
![]() keine differenzierbare Parametrisierung.
Aber wir können die
keine differenzierbare Parametrisierung.
Aber wir können die
![]() vermöge
vermöge
![]() ,
,
![]() umparametrisieren. Wegen
umparametrisieren. Wegen
![]() und
und
![]() können wir
können wir
![]() bilden. Wegen
bilden. Wegen
![]() verschwindet
verschwindet
![]() und den Randpunkten und somit ist
und den Randpunkten und somit ist
![]()
![]() .
Also können wir den Polygonzug
.
Also können wir den Polygonzug
![]() parametrisieren.
Es geht sogar
parametrisieren.
Es geht sogar
![]() , wenn wir
, wenn wir
![]() so wählen, daß alle Ableitungen am Rand
des Intervall verschwinden.
so wählen, daß alle Ableitungen am Rand
des Intervall verschwinden.
Beweis.
Eindeutigkeit:
Es seien
![]() für
für
![]() zwei Stammfunktionen.
Dann ist die Differenz
zwei Stammfunktionen.
Dann ist die Differenz
![]() differenzierbar mit Ableitung
differenzierbar mit Ableitung
![]() .
Sei
.
Sei
![]() und
und
![]() in
in
![]() beliebig und
beliebig und
![]() eine
eine
![]() -Kurve in
-Kurve in
![]() , die
, die
![]() mit
mit
![]() verbindet.
Dann ist
verbindet.
Dann ist
![]() .
.
(
![]() )
Umgekehrt sei
)
Umgekehrt sei
![]() beliebig und
beliebig und
![]() eine
eine
![]() -Kurve die
-Kurve die
![]() mit
mit
![]() verbindet. Dann setzen wir
verbindet. Dann setzen wir
![]() .
Für
.
Für
![]() sei weiters
sei weiters
![]() . Dann ist
. Dann ist
![]() für alle kleinen
für alle kleinen
![]() und
und
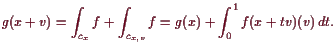
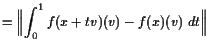 |
||
Beispiel.
Es sei die 1-Form
![]() gegeben durch
gegeben durch
![]() , wobei
, wobei
Wir können einen beliebigen Punkt
![]() durch die affine
durch die affine
![]() -Kurve
-Kurve
![]() mit
mit
![]() verbinden.
Also ist
verbinden.
Also ist
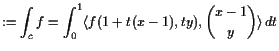 |
||
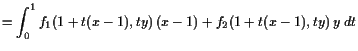 |
||
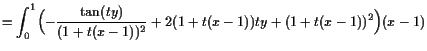 |
||
Wir können aber auch Achsen-parallele Wege verwenden:
Ebenso können wir folgende Achsen-parallele Wege verwenden:
Andreas Kriegl 2002-07-01