20.5 Komplexe Kurven-Integrale

In diesem Abschnitt seien alle Vektorräume $E$, $F$ etc. über den Körper $\mathbb{C}$ der komplexen Zahlen.

20.5.1 Lemma.
Es sei $f:\mathbb{C}\supseteq U\to F$ $C^2$ und $\mathbb{C}$-differenzierbar, dann ist $\frac{df}{dz}:U\to F$ ebenfalls $\mathbb{C}$-differenzierbar.

Wir werden in (20.5.10) zeigen, daß $\mathbb{C}$-differenzierbare Abbildungen $C^{\infty}$-sind, also sind auch all ihre Ableitungen $\mathbb{C}$-differenzierbar.

Beweis. Wir müssen zeigen, daß $\left(\frac{df}{dz}\right)'(z)$ $\mathbb{C}$-linear ist. Sei also $\lambda \in\mathbb{C}$. Dann ist

$$\left(\frac{df}{dz}\right)'(z)(\lambda \cdot v) = (f')'(z)(\lambda \cdot v)(1) = f''(z)(\lambda \cdot v,1)$$

$$= f''(z)(1,\lambda \cdot v)$$

$$= (f')'(z)(1)(\lambda \cdot v)$$

$$= \lambda \cdot (f')'(z)(1)(v) = \lambda \cdot (f')'(z)(v)(1)$$

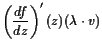$$= \lambda \cdot \left(\frac{df}{dz}\right)'(z)(v).{\rm\quad[]}$$

20.5.2 Satz über gewöhnliche komplexe Differentialgleichung.
Es sei $f:\mathbb{C}\times E\supseteq U\to E$ $C^1$ und in beiden Variablen $\mathbb{C}$-differenzierbar. Dann existiert lokal eine $\mathbb{C}$-differenzierbare Funktion $g:\mathbb{C}\to E$ mit $g'(x)=f(x,g(x))$ und $g(0) = 0$.

Beachte, daß wenn $f$ noch $\mathbb{C}$-differenzierbar von weiteren Parametern abhängt, so gilt dies auch für die Lösung und diese hängt auch $\mathbb{C}$-differenzierbar von den Anfangsdaten ab.

Beweis. Wir wenden den Satz von Frobenius auf die Funktion $\bar f:\mathbb{R}^2\times E\supseteq U\to L(\mathbb{R}^2,E)$, $z\mapsto (\lambda \mapsto \lambda \cdot f(z))$ an. Die Integrabilitätsbedingung ist erfüllt, denn

$$w\cdot f'(x,g(x)) (v,v\cdot f(x,g(x))) =$$

$$= w\cdot\Bigl(\d _1 f(x,g(x))(v) + \d _2 f(x,g(x))(v\cdot f(x,g(x)))\Bigr)$$

$$= w\cdot v\cdot \Bigl(\d _1 f(x,g(x))(1) + \d _2 f(x,g(x))(f(x,g(x)))\Bigr)$$

ist symmetrisch in $v$, $w$. Also existiert nach dem Satz von Frobenius eine lokale $C^1$ Lösung $g:\mathbb{R}^2\to E$ von

$$g'(x) = \bar f(x,g(x)).$$

Da $\bar f(z)$ nach Konstruktion $\mathbb{C}$-linear ist, ist $g$ $\mathbb{C}$-differenzierbar.     []

20.5.3 Folgerung. Komplexe Stammfunktion.
Es sei $f:\mathbb{C}\supseteq U\to F$ $\mathbb{C}$-differenzierbar auf der sternförmigen Menge $U$, dann existiert eine $\mathbb{C}$-differenzierbare Stammfunktion $g$ von $f$.

Beweis. Dazu müssen wir nur die Differentialgleichung $g'(z)=f(z)$ lösen, diese hat nach (20.5.2) eine $\mathbb{C}$-differenzierbare Lösung.     []

Zu $f:E\supseteq X\to \mathbb{C}$ definieren wir eine 1-Form $\tilde f:E\supseteq X\to \mathbb{C}\cong L_{\mathbb{C}}(\mathbb{C},E)\subseteq L(\mathbb{R}^2,E)$ durch $\tilde f(x)(\lambda ):= \lambda \cdot f(x)$. Dabei bezeichnet $L_{\mathbb{C}}(\mathbb{C},E)$ die $\mathbb{C}$-linearen (stetigen) Abbildungen $\mathbb{C}\to E$.

20.5.4 Satz. Komplexe Kurvenintegral.
Es sei $c:[a,b]\to\mathbb{C}$ $C^1$ und $f:\mathbb{C}\supseteq c([a,b])\to \mathbb{C}$ stetig. Dann existiert

$$\int_c f(z) dz := \int_c f := \int_c \tilde f$$

Ist $f=u+i v$, so ist

$$\int_c f = \int_c u dx-v dy\; + \;i \int_c v dx + u dy.$$

Weiters ist

$$\int_cf = \int_a^b f(c(t))\cdot c'(t)\;dt.$$

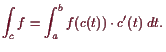
Beweis. Aus $\tilde f(z)(w):=w\cdot f(z)$, $f=:u+i v$ und $w=:x+i y$ folgt

$$\tilde f(z)(w) = (x+iy)\cdot (u(z)+iv(z))$$

$$= x\cdot \biggl(u(z) + i v(z)\biggr) + y\biggl(-v(z) + i u(z)\biggr)$$

$$= \biggl(x\cdot u(z) - y\cdot v(z)\biggr) + i\biggl(x\cdot v(z)+y\cdot u(z)\biggr)$$

und somit ist

$$\int_c f = \int_c \tilde f = \int_c (u + i v) dx + \int_c (i u - v) dy$$

$$= \int_c u dx + i \int_c v dx + i \int_c u dy - \int_c v dy$$

$$= \int_c (u dx -v dy) + i\int_c (v dx + u dy).$$

Für die letzte Gleichung sei $c=:x+i y$. Dann ist

$$\int_c f = \int_a^b \tilde f(c(t)) (c'(t))\;dt = \int_a^b \biggl(u(c(t))+i v(c(t))\biggr)\cdot (x'(t)+i y'(t)) dt$$

$$= \int_a^b (u\cdot x' -v\cdot y') + (u\cdot y'+v\cdot x') i dt$$

$$= \int_a^b (u\cdot x' -v\cdot y') dt + i \int_a^b (u\cdot y'+v\cdot x') dt$$

$$= \int_c u dx-v dy + i \int_c u dy + v dx$$

$$=: \int_c (u+i v)(dx +i dy) = \int_c f(z) dz{\rm\quad[]}$$

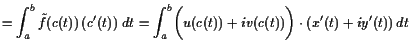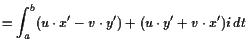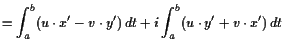Beispiel.
Für $f(z):=(z-z_0)^m$ mit $m\in\mathbb{Z}$ und der Parametrisierung $c(t):=z_0+r e^{it}$ für $t\in[0,2\pi]$ des Kreises mit Radius $r$ und Mittelpunkt $z_0$ ist

$$\int_c f = \left\{\begin{array}{ll} 0 &\text{für }m\ne 1 \\ 2\pi i &\text{für }m=1 \end{array}\right..$$

In der Tat ist

$$\int_c f = \int_0^{2\pi} (r(\cos(t)+i \sin(t)))^m r i e^{it} dt$$

$$= \int_0^{2\pi} r^{m+1} i e^{it(1+m)} dt = \int_0^{2\pi} r^{m+1} i \Bigl(\cos(t(m+1))+i\sin(t(m+1))\Bigr)$$

$$= \left\{\begin{array}{ll} \int_0^{2\pi} i dt = 2\pi i \text{ für... ...int_0^{2\pi(m+1)} \frac{\sin(t)}{m+1} dt = 0 \text{ sonst}.\end{array}\right.$$

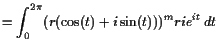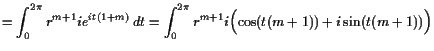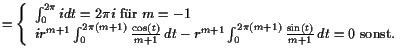20.5.5 Cauchy'sche Integralsatz.
Es sei $f:\mathbb{C}\supseteq U\to\mathbb{C}$ $\mathbb{C}$-differenzierbar und $U$ sternförmig. Dann ist $\int_c f$ wegunabhängig.

Beweis von (20.5.5). Jedes $f:\mathbb{C}\supseteq U\to\mathbb{C}$ definiert eine 1-Form $\bar f:U\to \mathbb{C}\hookrightarrow L(\mathbb{C},\mathbb{C})$ vermöge $\bar f(z)(v)=f(z)\cdot v$. Falls $f$ $\mathbb{C}$-differenzierbar ist, so erfüllt $\bar f$ die Integrabilitätsbedingung, da $\bar f'(z)(v)(w)=\frac{df}{dz}(z)\cdot v\cdot w$. Also folgt aus (20.4.4), daß $\bar f$ exakt ist und aus (20.4.5), daß das Kurvenintegral wegunabhängig ist.     []

20.5.6 Satz von Morera.
Vgl. (20.5.11) Es sei $f:\mathbb{C}\supseteq U\to\mathbb{C}$ stetig, $U$ zusammenhängend und $\int_c f$ wegunabhängig. Dann ist $g(z):=\int_c f$, wobei $c$ eine Kurve ist, die $z_0$ mit $z$ verbindet, eine $\mathbb{C}$-differenzierbare Stammfunktion. Für jede Stammfunktion $g$ von $f$ gilt: $\int_c f=g(c(b))-g(c(a))$.

Beweis. Aus (20.4.8) folgt die Existenz der Stammfunktion, und da deren Ableitung $f$ $\mathbb{C}$-linear ist, ist sie $\mathbb{C}$-differenzierbar nach (19.2.13).     []

20.5.7 Hilfssatz.
Es sei $f$ auf einen Kreisring $R$ $\mathbb{C}$-differenzierbar und $c_i$ für $i=1,2$ die beiden positiv durchlaufenen Randkreise. Dann ist $\int_{c_1} f=\int_{c_2}f$.

Beweis. Da das Kurvenintegral lokal wegunabhängig ist, können wir das Integral über die äußere Peripherie durch jenes über die Innere ersetzen (der zweimal verschieden orientierte Verbindungsweg trägt nichts bei). Also verschwindet das Integral über den gesamten (richtig durchlaufenen) Rand.     []

Beachte, daß dieser Beweis auch funktioniert, wenn die Randkreise des Kreisrings nicht konzentrisch sind.

20.5.8 Cauchy'sche Integralformel.
Es sei $f$ $\mathbb{C}$-differenzierbar auf der offenen Menge $U$ und $K$ eine Kreisscheibe in $U$. Dann ist

$$f(z) = \frac1{2\pi i}\int_{\d K} \frac{f(\zeta )}{\zeta -z} d\zeta$$    für alle $z$ im Inneren von $K$$$,$$

wobei $\d K$ den 1-mal positiv orientiert durchlaufenen Rand von $K$ bezeichnet.

Beweis.

$$\frac1{2\pi i}\int_{\d K} \frac{f(\zeta )}{\ze... ...,d\zeta - \int_{\d K} \frac{f(\zeta )-f(z)}{\zeta -z} d\zeta \biggr).$$

Das letzte Integral ist wie folgt abschätzbar, da $\zeta \mapsto \frac{f(\zeta )-f(z)}{\zeta -z}$ $\mathbb{C}$-differenzierbar auf dem punktierten Gebiet $U\setminus\{z\}$ ist, und wobei $c$ ein kleinerer Kreis ist:

$$\biggl\Vert \int_{\d K} \frac{f(\zeta )-f(z)}{\zeta -z} d\zeta \biggr\Vert = \biggl\Vert \int_{c} \frac{f(\zeta )-f(z)}{\zeta -z} d\zeta \biggr\Vert$$

$$\leq \frac{V(c)}{\text{Radius von }c} \sup\{ \Vert f(\zeta )-f(z)\Vert:\zeta \in \text{Bild}(c)\}$$

$$= 2\pi \sup\{ \Vert f(\zeta ) -f(z)\Vert:\zeta \in (c)\}$$

$$\to 0 \to 0.{\rm\quad[]}$$

20.5.9 Satz. Kurvenintegral ist stetig.
Es sei $c$ $C^1$, $f_n:c(I)\to \mathbb{C}$ stetig und konvergiere glm. gegen $f$, dann gilt:

$$\int_c f_n\to \int_c f.$$

Beweis. Wegen $\int_c f_n=\int_a^b f(c(t)) c'(t) dt$ folgt dies aus den entsprechenden Satz für einfach-Integrale.    []

20.5.10 Entwicklungssatz & Cauchy'sche Ableitungsformeln.

Es sei $f$ $\mathbb{C}$-differenzierbar, dann ist $f$ am Inneren der größten Kreisscheibe in $U$ um einen gegebenen Punkt in einen Potenzreihe entwickelbar. Jede $\mathbb{C}$-differenzierbare Funktion ist $C^{\infty}$ und

$$\frac{d^nf}{dz^n}(z) = \frac{n!}{2\pi i} \int_{\d K}\frac{f(\zeta )}{(\zeta -z)^{n+1}} dz.$$

Beweis. Aus (20.5.9) folgt wegen der glm. Konvergenz von

$$\frac1{\zeta -z} = \frac1{(\zeta - z_0)\left(1... ...} = \frac1{\zeta -z_0} \sum_k \left(\frac{z-z_0}{\zeta -z_0}\right)^k$$

für $\vert z-z_0\vert< \vert\zeta -z_0\vert$ und der Cauchy'schen Integralformel (20.5.8) die Gleichung

$$f(z) = \frac1{2\pi i}\int_c \frac{f(\zeta )}{\zeta -z} d\zeta = \frac1{2\pi i}\int_c \sum_k \frac{f(\zeta )}{(\zeta -z_0)^{k+1}}(z-z_0)^k d\zeta$$

$$= \sum_k (z-z_0)^k \frac1{2\pi i} \int_c \frac{f(\zeta )}{(\zeta -z_0)^{k+1}} d\zeta$$

Wir dürfen Differentiation und Integration unter den gegebenen Voraussetzungen miteinander vertauschen (siehe [Heuser, 128.2]) und erhalten somit die Existenz der Ableitungen von $f$ und die entsprechende Formel als Kurvenintegral für sie.     []

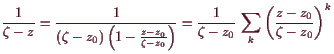
20.5.11 Satz von Morera.
Ist $f$ stetig mit wegunabhängigen Integral auf einer zusammenhängenden offenen Menge, so ist $f$ $\mathbb{C}$-differenzierbar.

Beweis. Nach (20.5.6) existiert eine $\mathbb{C}$-differenzierbare $g$ Stammfunktion, nach (20.5.10) ist $g$ $C^{\infty}$ und wegen (20.5.1) ist $f=g'$ $\mathbb{C}$-differenzierbar.     []

20.5.12 Satz. Holomorphie via Potenzreihen.
Es sei $I\subseteq \mathbb{R}$ offen, dann ist $f:I\to\mathbb{R}$ genau dann in eine Potenzreihe lokal um $z_0\in I$ entwickelbar, wenn es eine $\mathbb{C}$-differenzierbare Fortsetzung auf eine Umgebung von $z_0$ in $\mathbb{C}$ gibt.

Beweis. ( $\Leftarrow$) nach (20.5.10).

( $\Rightarrow$) Nach (19.2.3) konvergiert die Potenzreihe auch für komplexe Argumente. Die Summenfunktion ist dann wegen (19.2.10) $\mathbb{C}$-differenzierbar.     []

20.5.13 Identitätssatz für komplex-differenzierbare Funktionen.
Falls zwei $\mathbb{C}$-differenzierbare Funktionen auf einer zusammenhängenden Menge auf einer in der Menge konvergenten Folge übereinstimmen, so sind sie ident.

Beweis. Wir betrachten die Menge aller Punkte, die eine Umgebung besitzen auf der $f=g$. Der Grenzwert $z_{\infty}$ gehört zu dieser Menge wegen dem Identitätssatz für Potenzreihen (19.2.10). Die Menge ist nach Definition offen und sie ist abgeschlossen, aus dem gleichen Argument wie für $z_{\infty}$. Da der Definitionsbereich zusammenhängend ist, ist diese Menge der ganze Bereich, denn das Urbild dieser Menge unter einer stetigen Kurve wäre dann offen und abgeschlossen in $[0,1]$ also ganz $[0,1]$.     []

20.5.14 Maximumprinzip.
Es sei $f$ auf einer zusammenhängenden Menge $\mathbb{C}$-differenzierbar und nicht konstant, dann besitzt $\Vert f\Vert$ kein Maximum.

Beweis. Es genügt zu zeigen, daß eine $\mathbb{C}$-differenzierbare Funktion $f:\mathbb{C}\supseteq U\to\mathbb{C}$, die ein Maximum $z_0$ besitzt, konstant ist. Sei also $\vert f(z)\vert\leq \vert f(z_0)\vert$ für alle $z\in U$. Wir zeigen zuerst, daß $\vert f(z)\vert=\vert f(z_0)\vert$. Dazu nehmen wir indirekt an, daß ein $z_1$ existiert mit $\vert f(z_1)\vert<\vert f(z_0)\vert$. Wir verbinden $z_0$ und $z_1$ mit einem Polygonzug $c$, und nehmen $t_0$ minimal, s.d. $\vert f(c(t_0))\vert=\vert f(z_0)\vert$. Sei $z_2:=c(t_0)$ Dann existiert beliebig nahe ein $z_3$ mit $\varepsilon :=\vert f(z_2)\vert-\vert f(z_3)\vert>0$. Sei $K$ der Kreis mit Mittelpunkt $z_2$ und Radius $r:=\vert z_3-z_2\vert$. Dann ist $\vert f(z)\vert<\vert f(z_2)\vert-\varepsilon /2$ für $z$ nahe $z_3$ (auf einen Bogen der Länge $\delta >0$) und somit ist

$$\vert f(z_2)\vert = \frac1{2\pi} \Bigl\vert\int_{\d K} \frac{f(\zeta )}{\zeta -z_2}... ...a (\vert f(z_2)\vert-\varepsilon /2) + (2\pi r-\delta ) \vert f(z_0)\vert\Bigr)$$

$$= \vert f(z_0)\vert - \frac{\delta \varepsilon }{4\pi r} < \vert f(z_0)\vert,$$

ein Widerspruch. Für den Rest benötigen wir folgenden Hilfssatz.     []

20.5.15 Hilfssatz.
Eine $\mathbb{C}$-differenzierbare Funktion ist genau dann konstant, wenn $\Vert f\Vert$ es ist.

Beweis. Für $\vert f\vert=0$ ist das trivial. Sei also $c^2:=\vert f\vert^2=u^2+v^2>0$ für $f=u+iv$. Dann ist

$$\d _1 u\cdot u + \d _1 v \cdot v = 0$$

$$\d _2 u\cdot u + \d _2 v \cdot v = 0$$

Wäre $f$ nicht konstant, so gäbe es nach (20.4.5) ein $z_0$ mit $f'(z_0)\ne 0$ und somit

$$0 \ne \det{f'(z)} =\d _1 u\cdot \d _2 v - \d _2 u \cdot \d _1 v.$$

Folglich hätte obiges lineares Gleichungssystem an der Stelle $z_0$ die eindeutige Lösung $u(z_0)=v(z_0)=0$. Wegen $u^2+v^2=c>0$ ist dies unmöglich.     []

20.5.16 Satz von Liouville.
Jede beschränkte $\mathbb{C}$-differenzierbare Funktion auf ganz $\mathbb{C}$ ist konstant.

Beweis. Aus $\Vert f\Vert _{\infty}<{\infty}$ für alle $z$ und der Cauchy'schen Formel (20.5.10) für einen Kreis um $z$ mit Radius $r$ folgt $\vert f'(z)\vert\leq \frac{\Vert f\Vert _{\infty}}{r}$. Mit $r\to{\infty}$ folgt $f'=0$ und somit ist $f$ nach (20.4.5) konstant.     []