VO 25099.1 and PS 25100.1 Dynamical systems and nonlinear differential equations

Lecturer: Prof. Henk Bruin

Email H. Bruin for further information for this course.

Proseminar by: Prof. Henk Bruin

Announcements

Easter Break is from 15 to 28 April
Pentacost is on June 8 & 9 (Vorlesungsfrei).

Exam (first opportunity) is planned on Wednesday June 26, 12:00-14:00, in HS02.

Exam (second opportunity) is planned on Friday July 19, 10:00-12:00, in HS03.

Exam (third opportunity) is planned on Thursday September 26, 10:00-12:00, in 6.140.

Exam (fourth opportunity) is planned on Friday Jnauary 10, 10:00-12:00, in 09.142.

Schedule

Day	Time	Room		from	until
Tuesday	13:15--14:45	HS02	Lecture	05.3.2019	26.06.2019
Wednesday	13:15-14:45	HS02	Lecture/Proseminar	7.3.2019	27.06.2019

Contents of the course

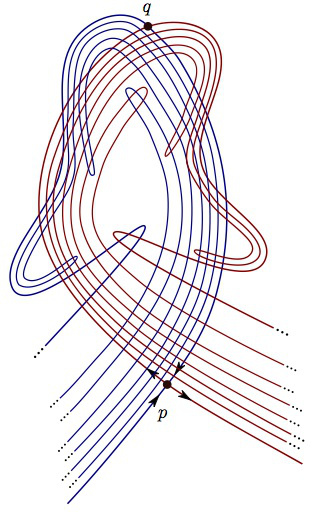
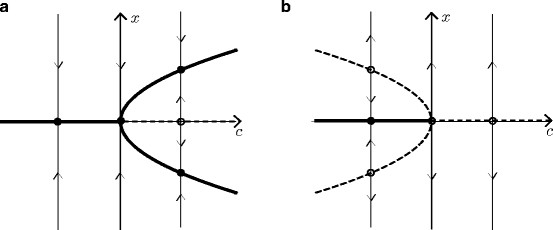
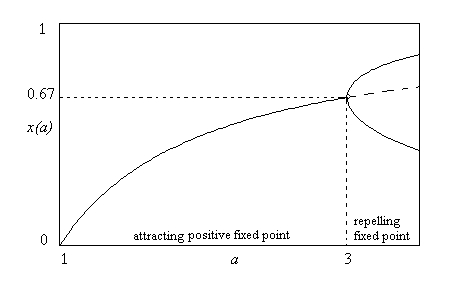
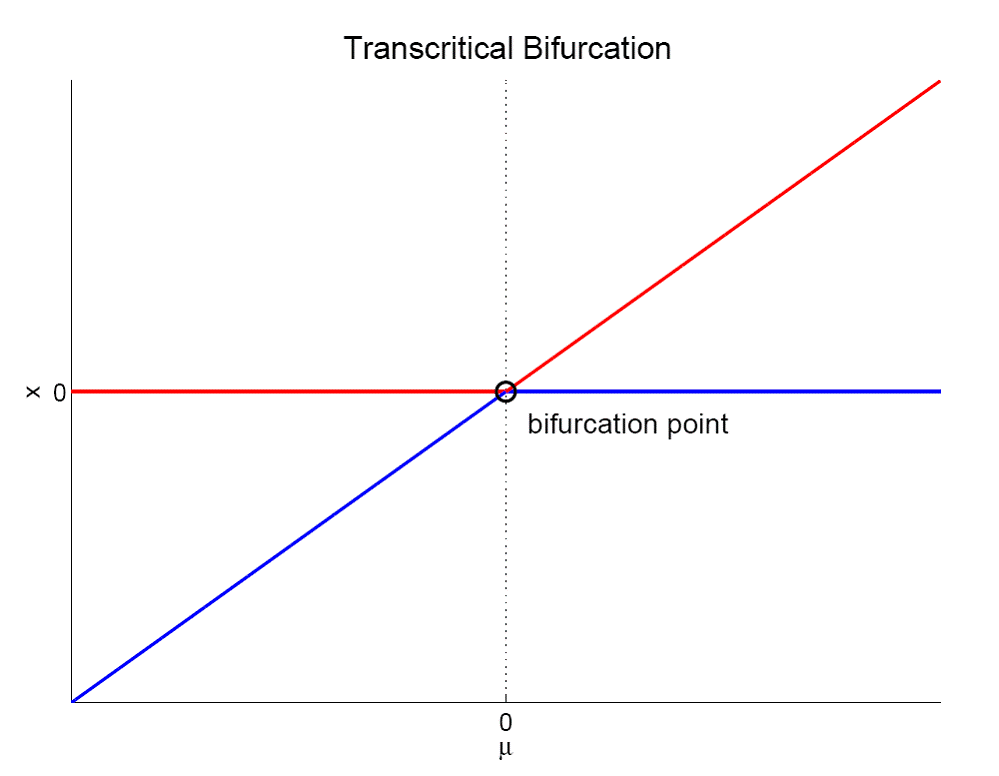
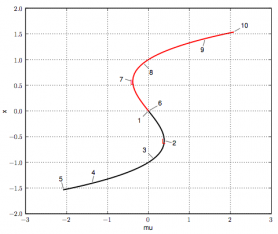
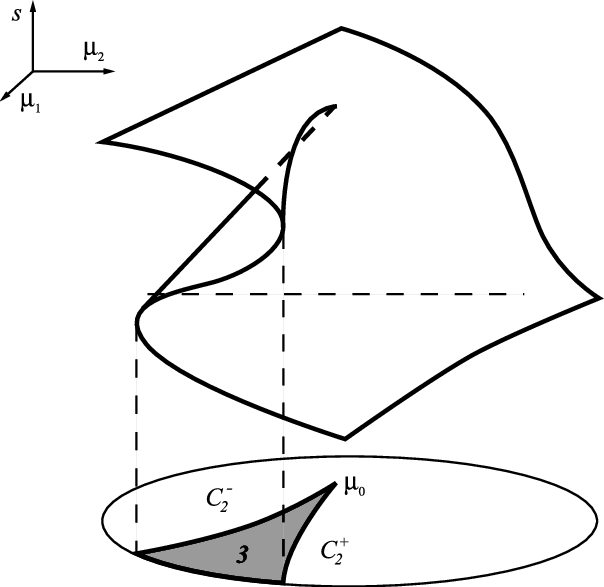
Basic notions for continuous and discrete dynamical systems; flows, attractors, and chaos; stability of stationary points by linearization and by Lyapunov functions, Poincaré-Bendixson theory, bifurcations.

The course will be given in English

Contents of the course (B = Exercises , S = Schmeiser's notes, T = Teschl's book), St = Strogatz lecture on youtube.

Bifurcations (S§5. T§6.5. T§11.1.)
Chaos (T§10.3)
Cusp bifurcation (S§5.4, St)
Existence, uniqueness, continuity of solutions of ODEs (S§1. T§2.2. T§2.4.)
Euler-Lagrange equations (T§8.3. S§10 and B)
Feigenbaum (bifurcation diagram) (S§6. T§11.1, St)
Hamiltonian systems (S§10. T§8.3. St and B)
Harmonic and other oscillators (S§8.3.)
Homoclinic orbits and tangles (S Def 10. T§13.2)
Hopf bifurcation (S§8.4. T p219-220)
Inhomogeneous linear ODEs (S§2.1. T§3.2.)
(In)stability of equilibria, sink, sources, saddles, centers (T§3.2.)
(In)stability of fixed points (T§6.5, T§10.2.)
Iteration of maps, cobweb diagrams (T§10.2.)
Kepler problem = two-body problem (T§8.5. S§10 and B )
Lagrangian = Lagrange function (T§8.3. S§10 and B )
Legendre transform (T§8.3. S§10 and B )
Limit cycles (S§8), see also Van der Pol equation and Poincaré-Bendixson.
Linear ODEs (S§2. T§3.2. T§3.3 St)
Linearization, the Hartman-Grobman theorem (S Thm 8. T§9.3.)
Logistic differential equation (T§10.1.)
Logistic (= quadratic) map (T§10.1. St)
Lorenz system (S§9. T§8.2., St and St)
Lotka-Volterra system (preditor-pray) T§7.1.
Lyapunov functions (S§7. T§6.6. St))
Orbits, omega-limit sets (T§6.3 T§8.1. S Def 4.)
Pendulum (T§6.7. S§10 (Example 8) and B .)
Phase portraits (T§3.2.)
Poincaré maps (T§6.4. T§12.2)
Poincaré-Bendixson Theorem (S§8.5. T§7.3, St)
Sensitive dependence on initial conditions (T§10.3)
Sharkovskiy's Theorem (T§11.2)
Smale's horseshoe (T§13.1.)
Stable/unstable manifolds (S Thm 7. T§9.2. T§12.3.)
Structural stability
Symbolic dynamics (T§11.5.)
Strange attractors (T§11.6.)
Van der Pol equations (S§8, T§7.2, St)

Weekly Progress

Symbolic dnamics, period 3 implies all periods
Sharkovkiy's Theorem

Day	Material
Week 1
5/3/2019	Introduction, 1-D ODEs, Stationary points and their stability Logistic ODEs vs. Logistic map
6/3/2019	Two-dimensional linear ODEs
Week 2
12/3/2019	No class (Rektorstag) Logistic ODEs vs. Logisitc map
13/3/2019	Proseminar: Exercises 1-5
Week 3
19/3/2019	structural stability
20/3/2019	Hartman-Grobman
Week 4
26/3/2019	bifurctions (transcritical, saddlenode/fold,pitchfork)
27/3/2019	Proseminar: Exercises 6-11
Week 5
2/4/2019	bifurcations (period doubling, cusp + hysteresis)
3/4/2019	mathematical chaos, Lyapunov exponents, sensitive dependence
Week 6
9/4/2019
10/4/2019	Proseminar: Exercises 6b,c, 10,11,12,14
Week 7
30/4/2019	Limit cykels, Van der Pol equation
1/5/2019	No class (Labour Day)
Week 8
7/5/2019	Poincaré-Bendixson Hopf bifurcation
8/5/2019	Test 1 (material up to Exercise 12) Proseminar: Exercises 14,15,16,17
Week 9
14/5/2019	Lotka-Volterra system Lyapunov functions
15/5/2019	Hamiltonian and Lagrangian dynamics Legendre transform
Week 10
21/5/2019	Noether's Theorem
22/5/2019	Proseminar: Exercises 16, 17, 18, 19, 20.
Week 11
28/5/2019	Integrable systems n-body problem
29/5/2019
Week 12
4/6/2019	Smale's horseshoe Homoclinic bifurcation
5/6/2019	Proseminar: Exercises 7-11
Week 13
11/6/2019	No class Vorlesungsfrei
12/6/2019	Circle homeomorphisms Sascha Troscheit replaces me
Week 14
18/6/2019	Lorenz attractors
19/6/2019	Proseminar Test 2: all exercises up to 20 and Exercises 7-11 New exercises: Exercises 21,22,26
Week 14
25/6/2019
26/6/2019	Exam (12:00--14:00 in HS02)

References/Background Reading

Kathy Alligood, Tim Sauer and James Yorke, Chaos, an Introduction to Dynamical Systems, Springer 1996 ISBN 0-387-94677-2
Michael Brin and Garrett Stuck, Introduction to Dynamical Systems, Cambridge University Press 2002 ISBN 0-521-80841-3
Robert Devaney, An Introduction to Cahotic Dynamical Systems, Benjamin and Cummings Publishing 1986, ISBN 0-8053-1601-9
Clark Robinson, Dynamical Systems (Stability, Symbolic Dynamics, and Chaos), CRC Press 1995 ISBN 0-8493-8493-1.
Steven Strogatz, Nonlinear dynamics and chaos, with applications to physics, biology and engineering, CRC Press, 2015, ISBN-13: 978-0813349107 or ISBN-10: 0813349109
G. Teschl, Ordinary Differential Equations and Dynamical Systems ODE Classnotes (or in fact book).

Assessment

Assessment of the course will be based on an written exam.

Assessment of the course proseminar will be based on two class tests (30 minues, worth 1/3) and the performance in class (solving exercises at the board), worth 1/3.

Course material (Hand-outs)

Class notes in pdf (written by Christian Schmeiser)
Exercises for the Proseminar.
An Applet for cobweb diagrams for the logistic family.
An Applet for the bifurcation diagram for the logistic family. Also this one .
One applet and another about period doubling bifurcations in the logistic family.
Hand-out about structural stability

Some bifurcation diagrams:


Pitchfork bifurcation	Period doubling bifurcation	Transcritical bifurcation

Spruce budworm (Caterpillar and Moth)	Two saddle node (= fold) bifurcations meeting in a cusp (x,k)-plane	Bifurcation surface for cusp (projecting to (r,k)-plane

as well as a lecture by Strogatz on the same topic.

half

Some phase portraits for the Van der Pol oscillator:

and also some youtube videos here, here, and a lecture by Strogatz (Cornell University).
Some youtube videos on Huygens resonance here, here, here, and here, and if you still didn't have enough, also here.
Some youtube videos on Smale and his horseshoe: here and here.


Smale's horseshoe	A homoclinic tangle	Another homoclinic tangle

Some youtube videos on Lorenz and the Lorenz attractor here, here, here, here and the Wikipedia page
Some youtube videos on three-body choreographies, here, here, and here and here. Or this one.
Some youtube videos on the Kepler problem (motion by the Earth and Sun), on gravitation, by Feynman (sort of), and general.
Online Lecture by Anima Nagar

Updated May 2 2019