Henk Bruin's Research Interests

Absolutely continuous invariant probabilities (acips) of interval maps
The long-term behaviour of chaotic dynamical systems can be described
statistically by means of invariant probability measures
m.
The frequency that typical orbits spend in a specified
subset of the phase space
tends to the measure of that subset (Birkhoff's Ergodic Theorem,
provided
m is ergodic).
"Typical" is related to the measure, but if the measure is absolutely
continuous with respect to Lebesgue measure (
m is an acip), then
the above holds for Lebesgue almost all points.
For smooth maps of the interval, finding acips is non-trivial, and is
in general connected to the growth rate of the derivative along the
orbits of the critical points.
A recurring theme in my research is the (non)existence of acips
when this growth rate is very small,
see e.g.
-
H. Bruin,
Topological conditions for the existence of invariant measures for
unimodal maps, Ergod. Th. and Dyn. Sys. 14 (1994)
433-451.
[.pdf]
-
H. Bruin,
The existence of absolutely continuous invariant measures is not a topological invariant for unimodal maps,
Ergod. Th.and Dyn. Sys. 18 (1998) 555-565.
[.pdf]
-
H. Bruin, S. van Strien,
Existence of acips for multimodal maps,
in Global Analysis of Dynamical Systems, Festschrift dedicated to
Floris Takens for his 60th birthday (2001)
[.pdf]
-
H. Bruin, W. Shen, S. van Strien,
Invariant measures exist without a growth condition,
Commun. Math. Phys. 241 (2003) 287-306
[.pdf]
The original publication is available at
[http://www.springerlink.com]
-
H. Bruin, W. Shen, S. van Strien,
Existence of unique SRB-measures is typical for unimodal
families,
Annales Scientifiques de l'ENS, 4e serie, 39 (2006) 381-414.
[.pdf]
-
H. Bruin, J. Rivera-Letelier, W. Shen, S. van Strien,
Large derivatives, backward contraction and invariant densities for interval
maps,
Inventiones Mathematicae 172 (2008), 509-533,
[.pdf]
The original publication is available at
[http://www.springerlink.com].
-
H. Bruin, M. Todd,
Complex maps without invariant densities,
Nonlinearity 19 (2006) 2929-2945.
Preprint (Version October 2006).
[.pdf]
Infinite measured systems
 There are many dynamical systems that do not preserve a finite
measure that is absolutely continuous with respect to the
reference measure (such as Lebesgue for interval maps).
Examples of such maps are the Manneville-Pomeau map, but also
certain (quadratic) interval maps.
In most cases, sigma-finite measures exist (although not always),
and in all cases the statistical properties of such measures are
strikingly different form what we understand in the probability
measure case.
There are many dynamical systems that do not preserve a finite
measure that is absolutely continuous with respect to the
reference measure (such as Lebesgue for interval maps).
Examples of such maps are the Manneville-Pomeau map, but also
certain (quadratic) interval maps.
In most cases, sigma-finite measures exist (although not always),
and in all cases the statistical properties of such measures are
strikingly different form what we understand in the probability
measure case.
-
H. Bruin, J. Hawkins,
Examples of expanding C1
maps having no sigma-finite
invariant measure equivalent to Lebesgue,
Isr. J. Math. 108 (1998) 83-107,
[.pdf]
- J. Al-Khal, H. Bruin, M. Jakobson,
New examples of S-unimodal maps with a sigma-finite absolutely continuous
invariant measure,
Discrete and Continuous Dynamical Systems, 22 no. 1-2, (2008) 35 - 61,
see
[here] for journal's version.
Earlier preprint version in
[.pdf]
- H. Bruin, M. Jakobson, and appendix by Genadi Levin,
New examples of topologically equivalent S-unimodal maps with different metric properties,
Contemp. Math. 469 2008 119-139.
[.pdf]
- H. Bruin, M. Todd,
Complex maps without invariant densities,
Nonlinearity 19 (2006) 2929-2945.
Preprint (Version October 2006).
[.pdf]
- H. Bruin, M. Nicol, D. Terhesiu,
On Young towers associated with infinite measure preserving transformations,
Stoch. and Dynamics, 9 (2009), 635 - 655,
in [.pdf], see also
World Scientific
Publishing Company
Statistical properties of non-uniformly hyperbolic dynamical systems
Ergodic theory of chaotic dynamical systems aims at describing the system
in terms of statistical laws that are frequently coming from
stochastic processes.
Laws that we would like to establish include the Central Limit Theorem,
decay of correlations (rates of mixing), return time statistics
to small sets, Bernoulli property (i.e. isomorphism to a Bernoulli process).
Operator theory and inducing techniques play an important role in
establishing such properties.
-
 H. Bruin, S. Luzzatto, S. van Strien, Decay of correlations in
one-dimensional dynamics, Preprint (1999) and (2001),
Ann. Sci. Ec. Norm. Sup. 36 (2003) 621-646,
[.pdf]
H. Bruin, S. Luzzatto, S. van Strien, Decay of correlations in
one-dimensional dynamics, Preprint (1999) and (2001),
Ann. Sci. Ec. Norm. Sup. 36 (2003) 621-646,
[.pdf]
-
H. Bruin,
Dimensions of recurrence times and minimal subshifts,
Conference Proceedings: from Chrystal to Chaos, Luminy
(2000),
[.pdf]
-
H. Bruin, Mark Holland, Ian Melbourne,
Subexponential decay of correlations for compact group extension of nonuniformly expanding systems,
Ergod. Th. & Dyn. Sys. 25 (2005) 1719-1738,
[.pdf]
-
H. Bruin, B. Saussol, S. Troubetzkoy, S. Vaienti,
Return time statistics via inducing,
Ergod. Th. Dyn. Sys. 23 (2003) 991-1013,
[.pdf]
-
H. Bruin, S. Vaienti,
Return time statistics for unimodal maps,
Fund. Math. 176 (2003) 77--94,
[.pdf]
-
H. Bruin, Mark Holland, Matt Nicol,
Livsic regularity for Markov Systems,
Ergod. Th. & Dyn. Sys. 25 (2005) 1739-1766,
[.pdf]
Equilibrium states
Equilibrium states are invariant measures that balance their potential
energy with their entropy content. This approach to selecting invariant mirrors ideas
from statistical mechanics.
The thermodynamic pressure is the supremum, taken over all invariant measures,
of the sum of potential energy and entropy.
Equilibrium states of Holder potentials of uniformly hyperbolic systems are fairly well understood; this theory goes back to Bowen, Ruelle and Sinai in the mid 1970s.
Since ca. 2000 the field has regained interest as the knowledge of nonuniformly hyperbolic systems increased with the advent of new tools, such as (Young) towers and Markov extensions.
<\br>
Our research shows existence and uniqueness of equilibrium states for
interval maps f and the natural potential -t log|Df|.
Also we show that the thermodynamic pressure
where f is an interval map.
Also we show that the thermodynamic pressure depends analytically on
the parameter t near t=1.
and equilibrium states, i.e. measures that maximize
the sum of there entropy nd the integral w.r.t. a specified potential function:
-
H. Bruin, G. Keller,
Equilibrium states for unimodal maps,
Ergod. Th. and Dyn. Sys. 18 (1998) 765-789,
[.pdf]
- H. Bruin, M. Todd,
Equilibrium states for interval maps: potentials
with sup φ - inf φ < h top(f),
Commun. Math. Phys. 283 (2008) 579-611.
DOI: 10.1007/s00220-008-0596-0.
The original publication is available at
this Springer site.
Preprint version of February 2008,
[.pdf]
- Henk Bruin, Mike Todd,
Equilibrium states for interval maps: the potential -t log |Df|.
Ann. Sci. Ecol Norm. Sup. 42 2009, 559-600.
Preprint version of January 2009:
[.pdf]
- H. Bruin, M. Todd
Transience and thermodynamic formalism for infinitely
branched interval maps
Preprint 2011 [.pdf].
Journal of the London Mathematical Society 86 2012, 171-194
DOI:
10.1112/jlms/jdr081
- H. Bruin, M. Todd
Wild attractors and thermodynamic formalism,
Preprint 2012 [.pdf]
- (with Renaud Leplaideur)
Renormalization, thermodynamic formalism and quasi-crystals in subshifts.
[.pdf]
Commun. Math. Phys. 321 (2013), 209-247.
DOI: 10.1007/s00220-012-1651-4
Attractors of chaotic dynamical systems
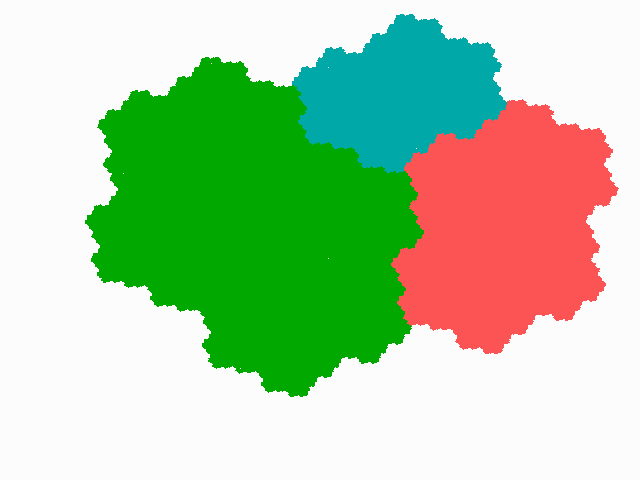 Attractors of one-dimensional systems can be more interesting than simply
stable periodic orbits. There are ways in which a Cantor set A can attract
Lebesgue a.e. point. One is the "solenoidal attractor", when the map
is infinitely renormalisable, the other is the "wild attractor", in which case
the second Baire category set of points is not attracted to A.
Thus A is only an attractor in a measure theoretic, but not
in a topological sense. The following paper deal with the properties of such attractors:
Attractors of one-dimensional systems can be more interesting than simply
stable periodic orbits. There are ways in which a Cantor set A can attract
Lebesgue a.e. point. One is the "solenoidal attractor", when the map
is infinitely renormalisable, the other is the "wild attractor", in which case
the second Baire category set of points is not attracted to A.
Thus A is only an attractor in a measure theoretic, but not
in a topological sense. The following paper deal with the properties of such attractors:
-
 H. Bruin, G. Keller, T. Nowicki, S. van Strien,
Wild Cantor attractors exist,
Annals of Math. 143 (1996) 97-130,
[.pdf]
H. Bruin, G. Keller, T. Nowicki, S. van Strien,
Wild Cantor attractors exist,
Annals of Math. 143 (1996) 97-130,
[.pdf]
-
H. Bruin, G. Keller, M. St. Pierre,
Adding machines and wild attractors,
Ergod. Th. and Dyn. Sys. 17 (1997) 1267-1287,
[.pdf]
- H. Bruin,
Topological conditions for the existence of Cantor attractors,
Trans. Amer.
Math. Soc. 350 (1998) 2229-2263,
[.pdf]
-
H. Bruin, J. Hawkins,
Exactness and maximal automorphic factors of unimodal maps,
Ergod. Th. and Dyn. Sys. 21 (2001) 1009-1034,
[.pdf]
-
H. Bruin, W. Shen, S. van Strien,
Existence of unique SRB-measures is typical for unimodal
families,
Annales Scientifiques de l'ENS, 4e serie, 39 (2006) 381-414,
[.pdf]
- H. Bruin, V. Jiménez-López,
On the Lebesgue measure of Li-Yorke pairs for interval maps
Preprint 2009,
[.pdf]
Commun. Math. Phys. 299 (2010), 523--560.
The final publication is available at
http://www.springerlink.com/content/fu01lpu5u4305572/.
(DOI: 10.1007/s00220-010-1085-9)
Symbolic dynamics
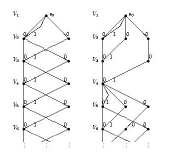
Symbolic descriptions are very common in symbolic dynamics,
leading to several classes of subshifts, such as
subshifts of finite type, sofic systems, Toeplitz shifts, substitution shifts,
etc. In my research, especially the latter plays a role in describing the
dynamics of maps restricted to certain minimal Cantor sets.
In fact, any minimal system on the Cantor set has
descriptions in terms of substitutions shifts, enumeration scales
as well as adic shifts on Bratteli diagrams.
-
H. Bruin,
Combinatorics of the kneading map,
Int. Jour. of Bifur. and Chaos 5 (1995) 1339-1349,
[.pdf]
-
H. Bruin,
Dimensions of recurrence times and minimal subshifts,
Conference Proceedings: from Chrystal to Chaos, Luminy
(2000),
[.pdf]
-
H. Bruin,
Minimal Cantor systems and unimodal maps,
J. Difference Eq. and Appl. 9 (2003) 305--318,
[.pdf]
-
H. Bruin, O. Volkova,
The complexity of Fibonacci-like kneading sequences,
Theo. Comp. Science. 377 (2005) 379-389,
[.pdf]
Topological dynamics of interval maps
 The combinatorial and topological properties of interval maps
and maps of the complex plane have an impact on their metric properties.
But also they are also interesting on their own accord, as they provided
new approaches to, e.g. the structure of minimal Cantor systems
within interval maps.
The combinatorial and topological properties of interval maps
and maps of the complex plane have an impact on their metric properties.
But also they are also interesting on their own accord, as they provided
new approaches to, e.g. the structure of minimal Cantor systems
within interval maps.
-
H. Bruin, G. Keller, M. St. Pierre,
Adding machines and wild attractors,
Ergod. Th. and Dyn. Sys. 17 (1997) 1267-1287,
[.pdf]
-
H. Bruin,
Homeomorphic restrictions of unimodal maps,
Contemp. Math. 246 (1999)
47-56,
[.pdf]
-
H. Bruin,
Minimal Cantor systems and unimodal maps,
J. Difference Eq. and Appl. 9 (2003) 305--318,
[.pdf]
- H. Bruin, V. Jiménez-López,
On the Lebesgue measure of Li-Yorke pairs for interval maps
Preprint 2009,
[.pdf]
- J. Bobok, H. Bruin,
The topological entropy of Banach spaces
Preprint 2011 [.pdf]
J. Difference Equ. Appl. 18 (2012), no. 4, 569-578.
Topological entropy of interval maps
 Topological entropy is a measure of the complexity of a map.
One outstanding question is how this depends on the parameters
in parametrised families of interval maps.
In the main conjecture from the 1980s in this area, namely that
entropy depends monotonically on the parameter in the logistic
family was solved by results of Milnor and Thurston, Sullivan, and
Douady and Hubbard. All these results use complex methods,
and a purely real proof is still unknown. In fact, monotonicity
fails for certain non-logistic families.
Some results of mine in this area, including the proof of monotonicity
of entropy (joint with Sebastian van Strien) for multimodal
polynomials are the following.
Topological entropy is a measure of the complexity of a map.
One outstanding question is how this depends on the parameters
in parametrised families of interval maps.
In the main conjecture from the 1980s in this area, namely that
entropy depends monotonically on the parameter in the logistic
family was solved by results of Milnor and Thurston, Sullivan, and
Douady and Hubbard. All these results use complex methods,
and a purely real proof is still unknown. In fact, monotonicity
fails for certain non-logistic families.
Some results of mine in this area, including the proof of monotonicity
of entropy (joint with Sebastian van Strien) for multimodal
polynomials are the following.
- H. Bruin,
Non-monotonicity of entropy of interval maps,
Phys. Lett. A 202 (1995) 359-362. Preprint version
[.pdf]
-
H. Bruin,
An algorithm to compute the topological entropy of a
unimodal map,
Proceedings contribution for the conference in memory of W. Szlenk,
Barcelona (1996)
Internat. J. Bifur. Chaos 9 (1999) 1881-1882,
[.pdf]
- H. Bruin, S. van Strien,
Monotonicity of entropy for real multimodal maps
Preprint 2009, revised version of December 2013 - Journ. Amer. Math. Soc.
28 (2015), no. 1, 1-61.
[.pdf]
- J. Bobok, H. Bruin,
Constant slope maps and the Vere-Jones classification.
Preprint 2016 [.pdf].
Entropy 18(6) , 234, 2016. DOI:10.3390/e18060234
Inverse limit spaces
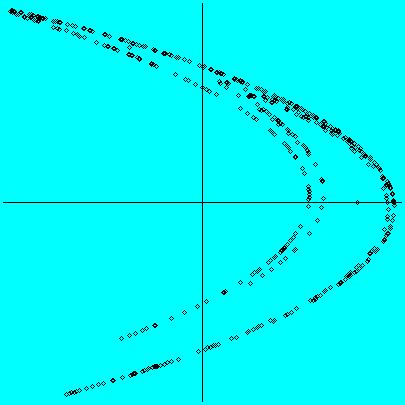
An inverse limit is a topological construction, which, briefly said,
consists of all backward orbits of a dynamical system equipped with a suitable topology. If the dynamical system is a unimodal (say quadratic) map, this
resulting space resembles to some extend the well-known Henon attractor
(see left).
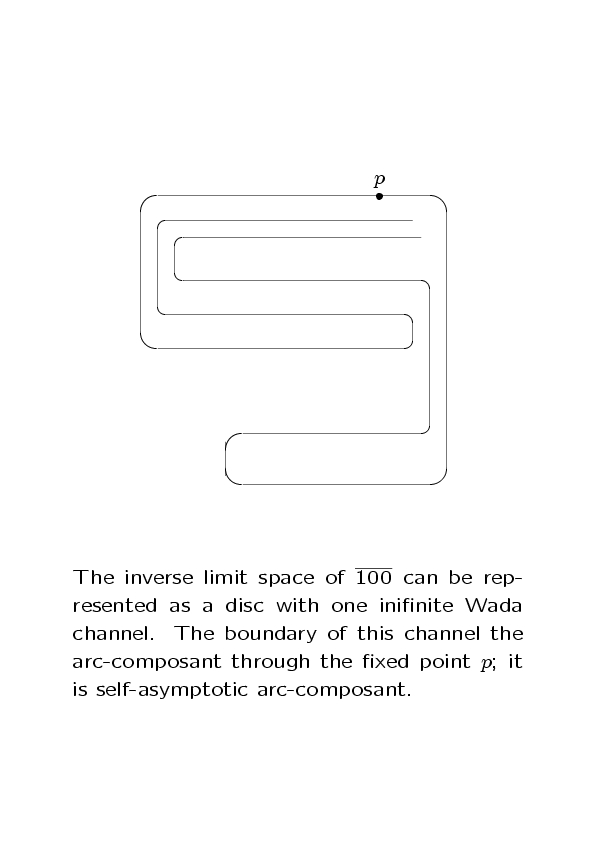 I view the study of unimodal inverse limit spaces as step towards studying
the topology of Henon attractors. Whereas Henon attractors are at least as
complicated as unimodal inverse limit spaces (with a single bonding map),
unimodal inverse limit spaces are sufficiently complicated themselves to
leave us with many questions.
Ingram's Conjecturm, i.e., the question of whether inverse limit
spaces
of non-conjugate bonding maps are always non-homeomorphic was solved
in 2009 in a joint paper by Marcy Barge, Sonja Stimac and me.
I view the study of unimodal inverse limit spaces as step towards studying
the topology of Henon attractors. Whereas Henon attractors are at least as
complicated as unimodal inverse limit spaces (with a single bonding map),
unimodal inverse limit spaces are sufficiently complicated themselves to
leave us with many questions.
Ingram's Conjecturm, i.e., the question of whether inverse limit
spaces
of non-conjugate bonding maps are always non-homeomorphic was solved
in 2009 in a joint paper by Marcy Barge, Sonja Stimac and me.
-
H. Bruin, K. M. Brucks,
Subcontinua of inverse limit spaces of unimodal maps,
Fund. Math. 160 (1999) 219-246,
[.pdf]
-
H. Bruin,
Planar embeddings of inverse limit spaces of unimodal maps,
Topology and its Applications 96 (1999) 191-208,
[.pdf]
-
H. Bruin,
Inverse limit spaces of post-critically finite tent maps,
Fund. Math. 165 (2000) 125-138,
[.pdf]
-
H. Bruin,
Asymptotic arc-components of unimodal inverse limit spaces,
Top. & Appl. 152 (2005) 182 - 200,
[.pdf]
- H. Bruin,
Subcontinua of Fibonacci-like unimodal inverse limit spaces,
Topology Proceedings 31 (2007) no. 1, 37-50.
[.pdf]
- M. Barge, H. Bruin, S. Stimac,
The Ingram Conjecture
[.pdf]
Geom. Topol. 16 (2012), 2481-2516.
- M. Barge, H. Bruin, L. Jones, L. Sadun,
Homological Pisot substitutions and exact regularity
Preprint 2010,
[.pdf]
Isr. J. Math. 188 2012, 281-300
(DOI) 10.1007/s11856-011-0123-4
- H. Bruin, S. Stimac,
On isotopy and unimodal inverse limit spaces
Preprint 2011, [.pdf],
Discrete and Continuous Dynamical Systems
32 (2012), no. 4, 1245-1253.
- H. Bruin, S. Stimac,
Entropy of homeomorphisms on unimodal inverse limit spaces,
[.pdf]
Nonlinearity 26 (2013) 991-1000.
Complex dynamics
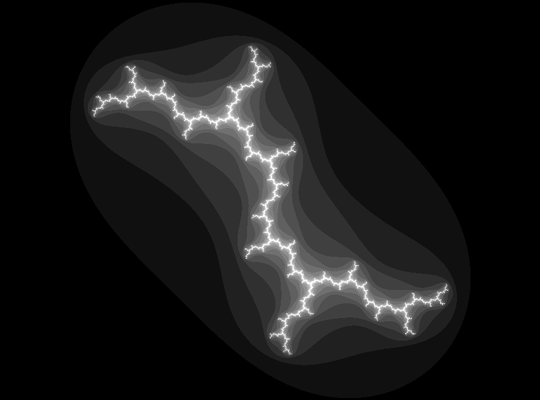
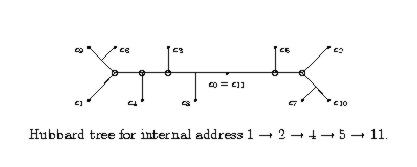 Julia sets of maps on the complex plane are a well-known source of fractals,
and especially for quadratic polynomials, there is a lot of literature, software and books about their Julia sets and the Mandelbrot set.
In joint work with Dierk Schleicher, we describe the underlying
combinatorial structure of complex quadratic polynomials, their symbolic
dynamics and Hubbard trees, external rays both in dynamic and parameter
space, and algorithms to connect them all.
Julia sets of maps on the complex plane are a well-known source of fractals,
and especially for quadratic polynomials, there is a lot of literature, software and books about their Julia sets and the Mandelbrot set.
In joint work with Dierk Schleicher, we describe the underlying
combinatorial structure of complex quadratic polynomials, their symbolic
dynamics and Hubbard trees, external rays both in dynamic and parameter
space, and algorithms to connect them all.
-
H. Bruin, D. Schleicher,
Symbolic dynamics of quadratic polynomials,
Preprint (2002)
This is available on the web-pages of the
Mittag-Leffler institute.
- H. Bruin, D. Schleicher,
Admissibility of kneading sequences and structure of Hubbard
trees for quadratic polynomials.
Journal Lond. Math. Soc. 78 (2008), no. 2, 502--522.
[.pdf]
- H. Bruin, A. Kaffl, D. Schleicher,
Existence of quadratic Hubbard trees.
Fund. Math. 202 (2009) 251-279,
[.pdf]
- H. Bruin, D. Schleicher,
Bernoulli measure of complex admissible kneading sequences,
Preprint 2012 [.pdf]
Ergod. Th. Dyn. Sys. 33 2013, 821-830.
DOI: 10.1017/edts.2012.134
Piesewise isometries
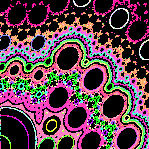 Piecewise isometries appear in applications ranging from digital data processing (Sigma-Delta-modulators), polygonal billiards and queuing theory.
Their dynamics is usually a mixture of (quasi)periodic and chaotic motion,
where it should be noted that the chaos is due o the discontinuities in the
system, rather than to positive Lyapunov exponents or positive entropy.
Piecewise isometries appear in applications ranging from digital data processing (Sigma-Delta-modulators), polygonal billiards and queuing theory.
Their dynamics is usually a mixture of (quasi)periodic and chaotic motion,
where it should be noted that the chaos is due o the discontinuities in the
system, rather than to positive Lyapunov exponents or positive entropy.
Except for a few special cases, which use number-theoretic peculiarities,
the behaviour of piecewise isometries poses many unanswered questions.
Already in dimension 1, there are piecewise isometries with very interesting properties, e.g. they can possess attractors of a multifractal nature, and
carrying multiple ergodic invariant measures.
-
H. Bruin, S. Troubetzkoy,
The Gauss map on a class of interval translation mappings,
Isr. J. Math. 137 (2003) 125-148,
[.pdf]
-
H. Bruin, A. Lambert, G. Poggiaspalla, S. Vaienti,
Numerical analysis for a discontinuous rotation of the torus,
Chaos 13 (2003) 558-571.
The original publication is available at
[http://www.springerlink.com]
-
H. Bruin,
Renormalisation in a class of interval translation
maps of $d$ branches,
Dynamical Systems, an international journal 22 (2007) 11 - 24.
Preprint version 2006,
[.pdf]
- H. Bruin, J. Deane,
Piecewise contractions are asymptotically periodic,
Proc. Amer. Math. Soc. 137 (2009), 1389-1395.
[.pdf]
- H. Bruin, G. Clack,
Inducing and unique ergodicity of double rotations
Preprint 2011 [.pdf],
Discrete and Continuous Dynamical Systems
32, no. 12 2012.
Click here for the electronic version of the journal.
Last modified: January 21 2017
This website is designed to be viewed with web
browsers that support
web
standards. The content of this page should still be accessible
on older browsers or other devices though visual formatting may be
basic.


There are many dynamical systems that do not preserve a finite
measure that is absolutely continuous with respect to the
reference measure (such as Lebesgue for interval maps).
Examples of such maps are the Manneville-Pomeau map, but also
certain (quadratic) interval maps.
In most cases, sigma-finite measures exist (although not always),
and in all cases the statistical properties of such measures are
strikingly different form what we understand in the probability
measure case.
 Attractors of one-dimensional systems can be more interesting than simply
stable periodic orbits. There are ways in which a Cantor set A can attract
Lebesgue a.e. point. One is the "solenoidal attractor", when the map
is infinitely renormalisable, the other is the "wild attractor", in which case
the second Baire category set of points is not attracted to A.
Thus A is only an attractor in a measure theoretic, but not
in a topological sense. The following paper deal with the properties of such attractors:
Attractors of one-dimensional systems can be more interesting than simply
stable periodic orbits. There are ways in which a Cantor set A can attract
Lebesgue a.e. point. One is the "solenoidal attractor", when the map
is infinitely renormalisable, the other is the "wild attractor", in which case
the second Baire category set of points is not attracted to A.
Thus A is only an attractor in a measure theoretic, but not
in a topological sense. The following paper deal with the properties of such attractors:
 H. Bruin, G. Keller, T. Nowicki, S. van Strien,
Wild Cantor attractors exist,
Annals of Math. 143 (1996) 97-130,
[.pdf]
H. Bruin, G. Keller, T. Nowicki, S. van Strien,
Wild Cantor attractors exist,
Annals of Math. 143 (1996) 97-130,
[.pdf]

 The combinatorial and topological properties of interval maps
and maps of the complex plane have an impact on their metric properties.
But also they are also interesting on their own accord, as they provided
new approaches to, e.g. the structure of minimal Cantor systems
within interval maps.
The combinatorial and topological properties of interval maps
and maps of the complex plane have an impact on their metric properties.
But also they are also interesting on their own accord, as they provided
new approaches to, e.g. the structure of minimal Cantor systems
within interval maps.
Topological entropy is a measure of the complexity of a map.
One outstanding question is how this depends on the parameters
in parametrised families of interval maps.
In the main conjecture from the 1980s in this area, namely that
entropy depends monotonically on the parameter in the logistic
family was solved by results of Milnor and Thurston, Sullivan, and
Douady and Hubbard. All these results use complex methods,
and a purely real proof is still unknown. In fact, monotonicity
fails for certain non-logistic families.
Some results of mine in this area, including the proof of monotonicity
of entropy (joint with Sebastian van Strien) for multimodal
polynomials are the following.

 I view the study of unimodal inverse limit spaces as step towards studying
the topology of Henon attractors. Whereas Henon attractors are at least as
complicated as unimodal inverse limit spaces (with a single bonding map),
unimodal inverse limit spaces are sufficiently complicated themselves to
leave us with many questions.
Ingram's Conjecturm, i.e., the question of whether inverse limit
spaces
of non-conjugate bonding maps are always non-homeomorphic was solved
in 2009 in a joint paper by Marcy Barge, Sonja Stimac and me.
I view the study of unimodal inverse limit spaces as step towards studying
the topology of Henon attractors. Whereas Henon attractors are at least as
complicated as unimodal inverse limit spaces (with a single bonding map),
unimodal inverse limit spaces are sufficiently complicated themselves to
leave us with many questions.
Ingram's Conjecturm, i.e., the question of whether inverse limit
spaces
of non-conjugate bonding maps are always non-homeomorphic was solved
in 2009 in a joint paper by Marcy Barge, Sonja Stimac and me.

 Julia sets of maps on the complex plane are a well-known source of fractals,
and especially for quadratic polynomials, there is a lot of literature, software and books about their Julia sets and the Mandelbrot set.
In joint work with Dierk Schleicher, we describe the underlying
combinatorial structure of complex quadratic polynomials, their symbolic
dynamics and Hubbard trees, external rays both in dynamic and parameter
space, and algorithms to connect them all.
Julia sets of maps on the complex plane are a well-known source of fractals,
and especially for quadratic polynomials, there is a lot of literature, software and books about their Julia sets and the Mandelbrot set.
In joint work with Dierk Schleicher, we describe the underlying
combinatorial structure of complex quadratic polynomials, their symbolic
dynamics and Hubbard trees, external rays both in dynamic and parameter
space, and algorithms to connect them all.
 Piecewise isometries appear in applications ranging from digital data processing (Sigma-Delta-modulators), polygonal billiards and queuing theory.
Their dynamics is usually a mixture of (quasi)periodic and chaotic motion,
where it should be noted that the chaos is due o the discontinuities in the
system, rather than to positive Lyapunov exponents or positive entropy.
Piecewise isometries appear in applications ranging from digital data processing (Sigma-Delta-modulators), polygonal billiards and queuing theory.
Their dynamics is usually a mixture of (quasi)periodic and chaotic motion,
where it should be noted that the chaos is due o the discontinuities in the
system, rather than to positive Lyapunov exponents or positive entropy.