Lösungen zu den Übungsaufgaben aus Abschnitt 7.2
Hier finden Sie alle Aufgaben aus Abschnitt 7.2 sowie ausgearbeitete Lösungen zu einigen der Aufgaben.
Aufgabe 7.2.4 (Lösung)
Bestimmen Sie den Vektor, der vom Punkt $A=(4,-9)$ zum Punkt $B=(-1,4)$ führt. Welcher Vektor führt von $B$ nach $A$? Wie hängen die beiden Vektoren zusammen?Aufgabe 7.2.5 (Lösung)
Eine Antenne einer Richtfunkstrecke ist auf einem Turm auf $47m$ Höhe montiert. Der Turm steht auf der Spitze eines $485m$ hohen Hügels. Die nächste Antenne der Richtfunkstrecke ist in $31m$ Höhe auf einem weiteren Turm montiert, der $4276m$ vom ersten entfernt auf $412m$ Seehöhe steht. Setzen Sie die beiden Antennen geeignet in das Koordinatensystem. Wie ist dann der Verbindungsvektor von der ersten Antenne zur zweiten Antenne?Aufgabe 7.2.7
Beweisen Sie explizit die Rechenregeln für $\R^2$ aus Proposition 7.2.6.Aufgabe 7.2.10 (Lösung)
Stellen Sie den Punkt $Q=(-2,8)$ als Linearkombination der Elemente $e_{1}$ und $e_{2}$ dar.Aufgabe 7.2.11 (Erweiterungsstoff) (Lösung)
Seien $u$ und $v$ zwei beliebige Elemente des $\R^{2}$. Wir sagen, dass $w\in\R^{2}$ dargestellt ist als Linearkombination von $u$ und $v$, wenn $$ w = \la u+\mu v $$ für $\la,\mu\in\R$. Stellen Sie $R=(-1,4)$ dar als Linearkombination von $A=(-3,-2)$ und $B=(2,5)$.Aufgabe 7.2.13 (Lösung)
Untersuchen Sie, ob die Punkte $R=(-4,-2)$, $S=(1,8)$ und $T=(4,7)$ jeweils auf $\overline{PQ}$, $s_{P:Q}$ und $g_{P:Q}$ liegen mit $P=(-1,4)$ und $Q=(2,10)$. Machen Sie eine Skizze, um die Lagebeziehungen auch zeichnerisch zu überprüfen. Wie verändern sich die Lagebeziehungen, wenn man $\overline{QP}$, $s_{Q:P}$ und $g_{Q:P}$ betrachtet?Aufgabe 7.2.15 (Lösung)
Seien $P$, $Q$ und $R$ drei Punkte. Beweisen Sie, dass $R\in s_{P:Q}$ genau dann, wenn es ein $\la\ge 0$ gibt mit $R=\la P+(1-\la)Q$.Aufgabe 7.2.18 (Lösung)
Überprüfen Sie jeweils, ob die angegebenen Paare von Vektoren kollinear sind.- $u=(1,3)$, $v=(4,12)$;
- $x=(12,4)$, $y=(2,6)$;
- $r=(1,4)$, $s=(1,6)$.
Aufgabe 7.2.22 (Lösung)
Wie ist jeweils die Lagebeziehung der folgenden Paare von Geraden? Falls die Geraden einander schneiden, bestimmen Sie den Schnittpunkt. Untersuchen Sie rechnerisch und zeichnerisch.- $g_{P:Q}$ und $g_{Rv}$ mit $P=(1,1)$, $Q=(4,-1)$, $R=(2,6)$ und $v=(1,5)$.
- $g_{Au}$ und $g_{Bw}$ mit $A=(-1,2)$, $u=(2,4)$, $B=(2,8)$ und $w=(-1,-2)$.
- $g_{Cx}$ und $g_{D:E}$ mit $C=(1,3)$, $x=(-1,3)$, $D=(0,6)$ und $E=(1,5)$.
Aufgabe 7.2.25 (Lösung)
Betrachten Sie die beiden Richtfunkantennen aus Aufgabe 7.2.5. Wie weit sind die Antennen voneinander entfernt?Aufgabe 7.2.28 (Erweiterungsstoff) (Lösung)
Seien $P,Q,R$ die Eckpunkte eines Dreiecks, und sei $S$ ein beliebiger Punkt in der Ebene. Beweisen Sie, dass es immer reelle Zahlen $\la$, $\mu$ und $\nu$ gibt mit $S=\la P+\mu Q+\nu R$ und $\la+\mu+\nu=1$. Das Tripel $(\la,\mu,\nu)$ nennt man die baryzentrischen Koordinaten von $S$ bezüglich des Dreiecks $D_{PQR}$. Zeigen Sie weiters, dass $S\in D_{PQR}$ genau dann, wenn $0\leq \la$, $0\leq\mu$ und $0\leq\nu$ gelten.Aufgabe 7.2.29 (Erweiterungsstoff) (Lösung)
Bestimmen Sie die baryzentrischen Koordinaten des Schwerpunktes (siehe [Kemnitz,p.114]) des Dreiecks $D_{PQR}$ mit $P=(1,1)$, $Q=(4,8)$ und $R=(2,5)$.Aufgabe 7.2.32 (Lösung)
Eine Schwimmboje soll durch eine gespannte Kette mit einem Poller am Ufer verbunden werden. Die Boje hat eine Höhe von $69cm$ und ist zu zwei Drittel untergetaucht. Die Befestigungsöse befindet sich an ihrer Spitze. Ebenfalls an der Spitze des $80cm$ hohen Pollers befindet sich die zweite Befestigungsöse. Der Poller steht am Ufer $1.5m$ über dem Wasserspiegel. Wie lang muss die Kette sein, dass sich die Schwimmboje mindestens $42m$ vom Ufer entfernen kann?Aufgabe 7.2.34
Beweisen Sie Proposition 7.2.33 explizit.Aufgabe 7.2.37 (Lösung)
Berechnen Sie die paarweisen Skalarprodukte der Vektoren $u=(1,4)$, $v=(-1,2)$, $w=(3,5)$ und $z=(-8,2)$.Aufgabe 7.2.39 (Lösung)
Weisen Sie explizit die Eigenschaften (IP1)–(IP3) des inneren Produkts nach.Aufgabe 7.2.41 (Lösung)
Beweisen Sie, dass Gleichheit in der Dreiecksungleichung $\|x+y\|\leq\|x\|+\|y\|$ genau dann gilt, falls die beiden Vektoren $x$ und $y$ kollinear und gleich orientiert sind oder einer der Vektoren der Nullvektor ist.Hinweis: Verwenden Sie die Cauchy–Schwarz Ungleichung und den Zusammenhang zwischen Norm und Skalarprodukt.
Aufgabe 7.2.44 (Lösung)
Berechnen Sie den Winkel zwischen den Vektoren $v=(-1,4)$ und $w=(9,5)$.Aufgabe 7.2.47 (Lösung)
Finden Sie drei Normalvektoren zum Vektor $w=(1,2)$. Wie sehen alle Normalvektoren auf $w$ aus?Aufgabe 7.2.48 (Lösung)
Spiegeln Sie den Punkt $R=(2,5)$ an der Geraden $g:=g_{P:Q}$ mit $P=(0,1)$ und $Q=(1,4)$. Gehen Sie dabei so vor, dass Sie die Gerade $h$ bestimmen, die durch $R$ geht und die normal auf $g$ steht. Schneiden Sie $g$ und $h$, und finden Sie den Punkt, der von $R$ doppelt so weit entfernt ist wie der Schnittpunkt von $g$ und $h$. Fertigen Sie auch eine Zeichnung an.Aufgabe 7.2.51 (Lösung)
Bestimmen Sie Geradengleichung und Hessesche Normalform für die folgenden Geraden:- $g_{P:Q}$ mit $P=(1,3)$ und $Q=(4,-2)$,
- $g_{Rv}$ mit $R=(-2,-3)$ und $v=e_{2}$,
- $g_{Sw}$ mit $S=(2,1)$ und $w=e_{1}$.
Aufgabe 7.2.54 (Lösung)
Bestimmen Sie den Normalabstand des Punktes $P=(3,6)$ von der Geraden $g_{Qv}$ mit $Q=(-1,2)$ und $v=(3,4)$.Aufgabe 7.2.55 (Lösung)
Wiederholen Sie Beispiel 7.2.48, indem Sie mit Hilfe der Hesseschen Normalform von $g$ einen zweiten Punkt auf der Normalen zu $g$ durch $R$ finden, der denselben Normalabstand von $g$ hat wie $R$.Aufgabe 7.2.57 (Lösung)
Gegeben sind die Punkte $A=(-2,-4)$, $B=(4,4)$, $C=(3,19)$ und $D=(-9,3)$. Prüfen Sie nach, dass $ABCD$ ein Trapez bildet. (Eines der beiden Paare von gegenüberliegenden Seiten muss zueinander parallel sein.) Berechnen Sie weiters die vier Winkel, den Umfang, den Flächeninhalt und die Höhe (den Abstand der parallelen Seiten).Aufgabe 7.2.60 (Lösung)
Schneiden Sie die Geraden $g_{1}:4x+3y=29$, $g_{2}:x-3y=19$ und $g_{3}:=g_{P:Q}$, für $P=(-1,3)$ und $Q=(8,4)$, mit dem Kreis $S_{5}(-2,4)$. Überprüfen Sie Ihre Ergebnisse zeichnerisch.Aufgabe 7.2.61 (Lösung)
Über einen kreisförmigen Teich mit $12m$ Durchmesser soll ein $80cm$ breiter Steg gebaut werden. Der Normalabstand der Mittellinie des Steges vom Mittelpunkt des Teiches soll $6m$ betragen. Die Stützen des Steges, die genauso breit wie der Steg sind, sollen außerhalb des Wassers mit $50cm$ Mindestabstand vom Ufer stehen. Wie weit sind die Stützen voneinander entfernt?Aufgabe 7.2.62 (Lösung)
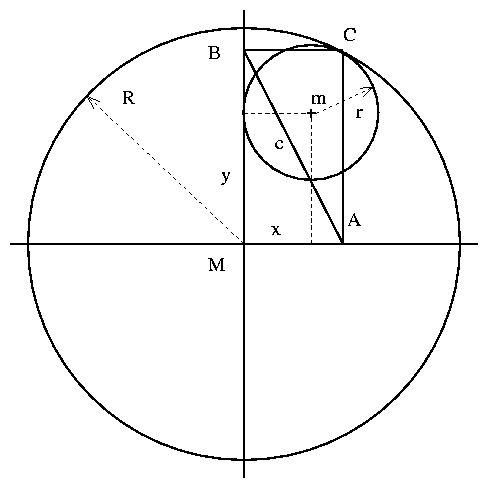
Einem Kreis mit Radius $R$, dessen Mittelpunkt $M$ im Ursprung liegt, ist ein kleinerer Kreis mit Radius $r$ eingeschrieben (siehe Skizze). Sein Mittelpunkt $m$ habe die Koordinaten $x$ und $y$. Der Berührpunkt $C$ der beiden Kreise ist einer der Eckpunkte eines achsenparallelen Dreiecks, dessen weitere Eckpunkte $A$ und $B$ auf den Achsen liegen. Bestimmen Sie die Länge der Seite $c$ dieses Dreiecks.
Aufgabe 7.2.64 (Lösung)
Rechnen Sie explizit nach, dass die Drehung $D_\ph$ in der Ebene eine lineare Abbildung ist, d.h. zeigen Sie explizit die Gültigkeit von (7.13).Aufgabe 7.2.65 (Lösung)
Zeigen Sie, dass für $\la\in\R$ die Abbildung $(x_{1},x_{2})\mapsto(\la x_{1},\la x_{2})$ linear ist.Aufgabe 7.2.67 (Lösung)
Weisen Sie explizit nach, dass die im Beweisteil (i) verwendete Tatsache $$A(x+y)=Ax+Ay\quad\text{und}\quad A(\la x)=\la Ax$$ für alle $A\in M_{2}(\R)$, $x,y\in\R^2$ und $\la\in\R$ gilt.Aufgabe 7.2.68
Rechnen Sie explizit nach, dass $(AB)x=A(Bx)$ gilt für $A,B\in M_{2}(\R)$ und $x\in\R^{2}$.Aufgabe 7.2.69 (Lösung)
Geben Sie die Matrixdarstellung der linearen Abbildung aus Aufgabe 7.2.65 an. Veranschaulichen Sie die geometrische Wirkung der Abbildung grafisch.Aufgabe 7.2.70 (Lösung)
Veranschaulichen Sie die geometrische Wirkung der linearen Abbildung, deren Matrixdarstellung $$ D = \begin{pmatrix} \mu & 0 \\ 0 & \nu \end{pmatrix} $$ ist.Aufgabe 7.2.71 (Lösung)
Sei $0\neq v\in\R^{2}$ gegeben. Betrachten Sie die Matrix $$ S_{v} := \mathbb{I} - \frac{2}{\|v\|^{2}} \begin{pmatrix} v_{1}^{2} & v_{1}v_{2} \\ v_{1}v_{2} & v_{2}^{2} \end{pmatrix}. $$ Welche geometrische Wirkung hat die lineare Abbildung, die von $S_{v}$ definiert wird? Untersuchen Sie dazu die folgenden Spezialfälle für $v$: $e_{1}$, $e_{2}$, $(1,1)$, $(-1,1)$. Gewinnen Sie daraus eine Vermutung, und beweisen Sie dann Ihre Vermutung.Hinweis: Betrachten Sie das Bild der Vektoren $e_{1}$, $e_{2}$, $(-v_{2},v_{1})$ auch graphisch.
Aufgabe 7.2.72 (Lösung)
Seien $S$ und $T$ zwei Spiegelungsmatrizen wie in Aufgabe 7.2.71. Zeigen Sie, dass $D=ST$ eine Drehung beschreibt. Um welchen Winkel wird gedreht?Aufgabe 7.2.74
Zeigen Sie dass für eine bijektive lineare Abbildung $f$ mit Matrixdarstellung $M_f$ die Inverse Abbildung $f^{-1}$ tatsächlich von der inversen Matrix $(M_f)^{-1}$ dargestellt wird, also dass $M_{f^{-1}}=(M_f)^{-1}$ gilt.Hinweis: Ziehen Sie ihre Aufzeichnungen zu Aufgabe 5.2.32 zu Rate.
