Dynamical systems and nonlinear differential equations

VO 250115-1 (5 ETCS) and PS 250010-1 (2 ECTS)

Lecturer: Prof. Henk Bruin

Email H. Bruin for further information for this course.

Proseminar by: Prof. Henk Bruin

Announcements

For Friday 1 March the lecture will be in HS8 at Oskar Morgensternplatz 1.
Please note also the change of lecture rooms for the rest of the semester.

The proseminar will be every other Friday, starting on March 8.

Rector's Day is March 12
Easter Break is from March 25 to April 7
Pentacost is on May 19 & 20 (Vorlesungsfrei).

Schedule

Day	Time	Room	from	to
Tuesday	16:45-18:15	SR8 Kolingasse	2.3.2024	27.06.2021
Friday Lecture (odd weeks)	11:30-13:00	SR7	19.3.2024	30.06.2021
Friday Proseminar (even weeks)	11:30-13:00	SR7	19.3.2024	30.06.2021

Weekly Progress

Day	Topic	Material
Week 1
1/3/2024	Introduction, 1-D ODE Stationary points and their stability simple polulation growth models	Notes of lecture 1 Lecture on a population dynamics model by Anima Nagar
Week 2
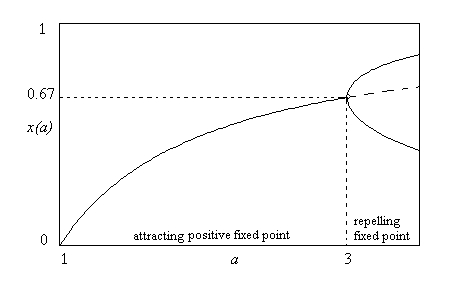
5/3/2024	Quadratic family Cobweb diagram Feigenbaum diagram	Notes of lecture 2. Applets used in the lecture: cobweb diagram, the bifurcation diagram and another one , all for the logistic family. Lecture by Strogatz A video on the Feigenbaum diagram. (Feigenbaum's constant is not part of the course material.)
8/3/2024	Proseminar	Exercise 1-5 of the Exercise sheet. The checkmark list on Moodle.
Week 3
12/3/2024	Rektorstag -- no class
15/3/2024	Class canceled
Week 4
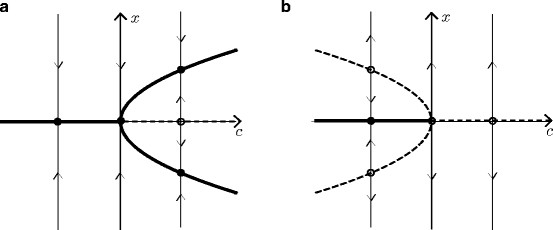
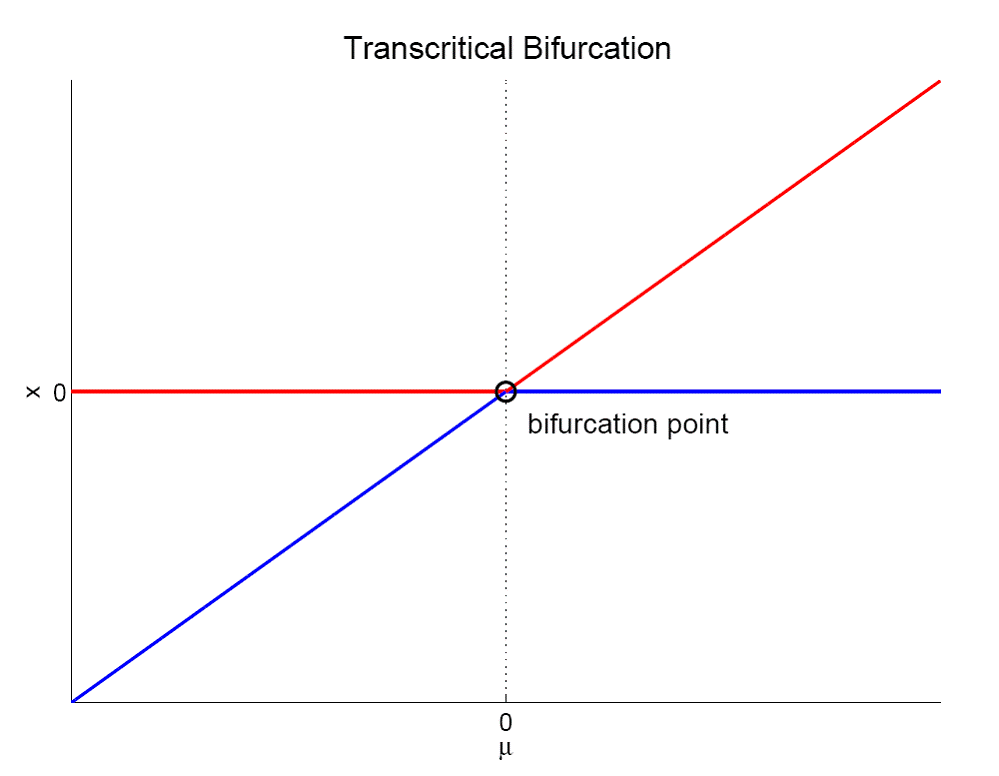
19/3/2024	Bifurcations in 1D
22/3/2024	Proseminar	Exercise 6,7,8,9 and 11 of the Exercise sheet. The checkmark list on Moodle.
Week 5
9/4/2024	Mathematical Chaos Topological transitivity	Notes of today's lecture
12/4/2024	Schwarzian Derivative	Notes of today's lecture
Week 6
16/4/2024	Hartman-Grobman	Notes of today's lecture Online lecture by Strogatz
19/4/2024	Proseminar	Exercise 11, 16, 17 and 18 of the Exercise sheet and also prove the following properties of the Schwarzian derivative (see also the lecture notes of April 12): 1. S(f o g) = (Sf) o g . (g')² - Sg. 2. Sf = 0 if and only if f is a Möbius transformation. Hint: Show that Sf = -2√(f') . (1/√(f'))''. Then Sf = 0 is equivalent to (1/√(f'))'' = 0, and that is easier to solve. The checkmark list on Moodle.
Week 7
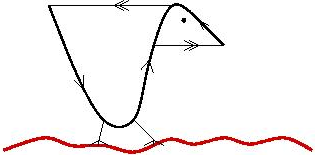
23/4/2024	Lotka-Volterra (predator-prey) systems Lyapunov functions.	Notes of today's lecture Lecture by Strogatz.
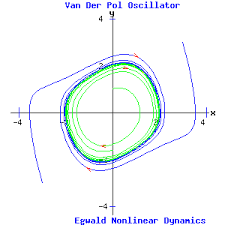
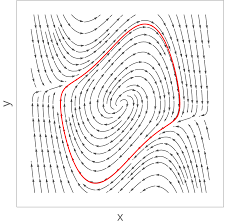
26/4/2024	Limit Cycles Van der Pol system ω-limit and α-limit sets
Week 8
30/4/2024	ω-limit and α-limit sets Poincaré-Bendixson Theorem
19/4/2024	Proseminar	Exercise 17 and 18 of the Exercise sheet and also prove the following properties of the Schwarzian derivative (see also the lecture notes of April 12): 1. S(f o g) = (Sf) o g . (g')² - Sg. 2. Sf = 0 if and only if f is a Möbius transformation. Hint: Show that Sf = -2√(f') . (1/√(f'))''. Then Sf = 0 is equivalent to (1/√(f'))'' = 0, and that is easier to solve. The checkmark list on Moodle.
Week 9
7/5/2024	Circle maps Rotation numbers	Notes of the today's lecture
10/5/2024	Rotation numbers Symbolic dynamics
Week 10
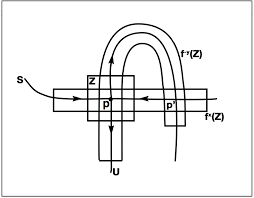
14/5/2024	Smale's horseshoe More symbolic dynamics	Notes of the today's lecture Nagar's Lecture 12 on dynamics of the horseshoe attractor.
17/5/2024	Proseminar	Exercise 18, 21 and 22 of the Exercise sheet and also prove the following properties of the Schwarzian derivative (see also the lecture notes of April 12): 1. S(f o g) = (Sf) o g . (g')² - Sg. 2. Sf = 0 if and only if f is a Möbius transformation. Hint: Show that Sf = -2√(f') . (1/√(f'))''. Then Sf = 0 is equivalent to (1/√(f'))'' = 0, and that is easier to solve. The checkmark list on Moodle.
Week 11
21/5/2024	Pentacost, no class
24/5/2024	Toral automorphisms	Lecture by Anima Nagar: Lectures 33 and Lecture 34 on chaos in hyperbolic toral automorphisms.
Week 12	Topological Entropy	Notes on topological entropy (Only Sections 1.3 and 1.4 are course material) Several lectures by Anima Nagar on entropy: Lecture 27 on measuring chaos, topological entropy. Lecture 28 on Adler's et al. definition of topological entropy. Lecture 29 on Bowen's definition of topological entropy. Lecture 30 on equivalence of the two definitions of topological entropy.
28/5/2024
31/5/2024	Proseminar	Exercise 41, 42, 43, 46 and 48 of the Exercise sheet
Week 13
4/6/2024	More on Topological Entropy	Notes on topological entropy (Only Sections 1.3 and 1.4 are course material)
7/6/2024	Oscillators and resonance driven, coupled oscialltors	Notes of today's lecture
Week 14
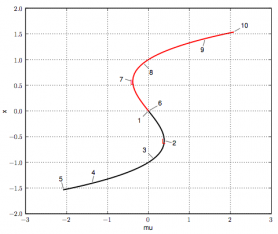
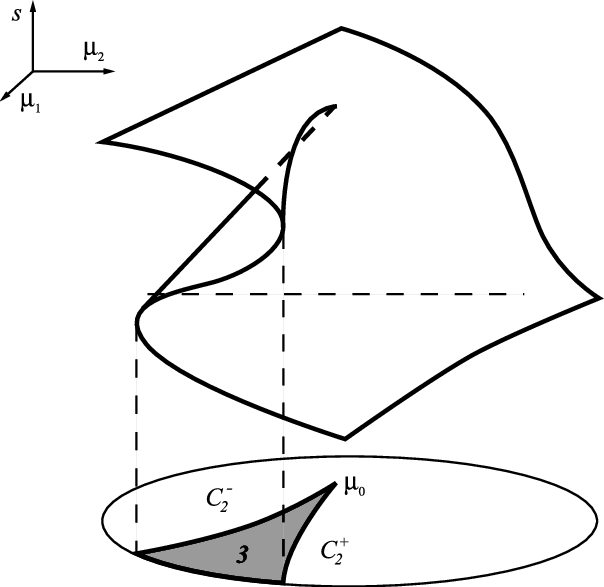
11/6/2024	The cusp bifurcation hysteresis	Notes of today's lecture. Class notes in pdf by Christian Schmeiser also cover the cusp bifurcation (as well as other bifurcations) in Section 5. Lecture by Strogatz.
14/6/2024	Proseminar	Exercises 40 and 48 of the Exercise sheet Furthermore: 1. Let A = {1,2,...,d} be an alphabet and Σ = A^N. Let (X = A^N,σ) be a subshift (i.e., X is a subset of Σ) with metric d(x,y) = 2^-n for n = min(k : x_k ≠ y_k). Let p(n) = #{subwords of length n in X}. a) Show that h_top(σ) = lim_n (log p(n))/n. b) What is the entropy of the full shift on d letters? c) Compute the entropy of a subshift of finite type with transition matrix A = (2 1 // 1 1) 2. Let R_α(x) = x+α mod 1 be an irrational rotation on the unit circle. Define symbolic dynamics based on the partition [0, α) with symbol 0 and [α, 1) with symbol 1. Let i:S¹ → {0,1}^N be the itinerary map. a) An n-cylinder Z[x] is defined as the set {y : i(y)_k = i(x)_k for 0 ≤ k < n}. What do n-cylinders look like as subset of the circle? b) How many n-cylinders does a circle rotation have? Derive the entropy of R_α from this.
Week 15
18/6/2024	No lecture
21/6/2024	No lecture
Week 16
25/6/2024	The Lorenz system	Notes of today's lecture Lectures by Strogatz on the Lorenz system and another one.
28/6/2024	Proseminar	Exercises 38, 51, 53, 55 of the Exercise sheet

References/Background Reading

Kathy Alligood, Tim Sauer and James Yorke, Chaos, an Introduction to Dynamical Systems, Springer 1996 ISBN 0-387-94677-2
Michael Brin and Garrett Stuck, Introduction to Dynamical Systems, Cambridge University Press 2002 ISBN 0-521-80841-3
Robert Devaney, An Introduction to Cahotic Dynamical Systems, Benjamin and Cummings Publishing 1986, ISBN 0-8053-1601-9
Clark Robinson, Dynamical Systems (Stability, Symbolic Dynamics, and Chaos), CRC Press 1995 ISBN 0-8493-8493-1.
Steven Strogatz, Nonlinear dynamics and chaos, with applications to physics, biology and engineering, CRC Press, 2015, ISBN-13: 978-0813349107 or ISBN-10: 0813349109
G. Teschl, Ordinary Differential Equations and Dynamical Systems ODE Classnotes (or in fact book).

Assessment

Assessment of the course will be by oral exam, as discussed in class. The default language is English, but German is possible too.

Course material (Hand-outs)

Exercise sheet in pdf
Class notes in pdf (written by Christian Schmeiser)
Exercises for the Proseminar.
An Applet for cobweb diagrams for the logistic family.
An Applet for the bifurcation diagram for the logistic family. Also this one .
One applet and another about period doubling bifurcations in the logistic family.
Hand-out about structural stability

Some bifurcation diagrams:


Pitchfork bifurcation	Period doubling bifurcation	Transcritical bifurcation

Spruce budworm (Caterpillar and Moth)	Two saddle node (= fold) bifurcations meeting in a cusp (x,k)-plane	Bifurcation surface for cusp (projecting to (r,k)-plane

as well as a lecture by Strogatz on the same topic.

half

Hand-out about symbolic itineraries
Some phase portraits for the Van der Pol oscillator:

and also some youtube videos here, here, and a lecture by Strogatz (Cornell University).
Arnol'd's catmap applet and another
Some videos about oscillators such as a driven pendulum, another one , and an inverted pendulum. Spectular outcome of resonance is demonstrated by Tacoma Bridge and in colour.
Some youtube videos on Huygens resonance here, here, here, and here, and if you still didn't have enough, also here.
Some youtube videos on Smale and his horseshoe: here and here.


Smale's horseshoe	A homoclinic tangle	Another homoclinic tangle

Some youtube videos on Lorenz and the Lorenz attractor here, here, here, here and the Wikipedia page
Written out class notes of June 18 in pdf.
Some youtube videos on three-body choreographies, here, here, and here and here. Or this one.
Some youtube videos on the Kepler problem (motion by the Earth and Sun), on gravitation, by Feynman (sort of), and general.
Some online source on the pendulum
Some online source on Hamiltonian/Lagragian/Newtonian mechanics
Online Lectures on Chaotic Dynamical Systems by Anima Nagar (Indian Institute of Technology, Delhi)

Preview
Lecture 1 general introduction and motivation of dynamical systems
Lecture 2 on elementary concepts.
Lecture 3 on periodic orbits, their hyperbolicity, stable/unstable sets, Schwarzian derivative.
Lecture 4 more on orbits.
Lecture 5 on periods of periodic points.
Lecture 6 on scrambled sets.
Lecture 7 on sensitive dependence on initial conditions.
Lecture 8 on a population dynamics model.
Lecture 9 on bifurcations, tent-maps and topological conjugacy.
Lecture 10 on nonlinear systems, solenoids, Smale's horseshoe.
Lecture 11 on horseshoe attractors.
Lecture 12 on dynamics of the horseshoe attractor.
Lecture 13 on recurrence.
Lecture 14 on recurrence continued.
Lecture 15 on transitivity.
Lecture 16 on Devaney chaos.
Lecture 17 on transitivity and Devaney chaos, Sharkovskiy's Theorem.
Lecture 18 on stronger forms of transitivity, mixing and weak mixing.
Lecture 19 on the chaotic properties of mixing systems.
Lecture 20 on weakly mixing and chaos.
Lecture 21 on strong transitivity and locally eventually onto.
Lecture 22 on stronger forms of transitivity continued.
Lecture 23 on introduction to symbolic dynamics.
Lecture 24 on symbolic dynamics, subshifts, continued fractions,
Lecture 25 on subshift of finite type.
Lecture 26 on subshift of finite type continued.
Lecture 27 on measuring chaos, topological entropy.
Lecture 28 on Adler's et al. definition of topological entropy.
Lecture 29 on Bowen's definition of topological entropy.
Lecture 30 on equivalence of the two definitions of topological entropy.
Lecture 31 on linear systems in dimension 2.
Lecture 32 on asymptotic properties of orbits of linear systems in dimension 2.
Lecture 33 hyperbolic toral automorphisms.
Lecture 34 on chaos in toral automorphisms.
Lecture 35 on attractors of the Hénon map.

Updated February 26 2024